题目内容
若不等式t2-log2xt<0对任意t∈(0,
]恒成立,则实数x的取值范围是( )
| 1 |
| 2 |
分析:通过构造函数,利用函数的图象推出x 的不等式求解即可.
解答: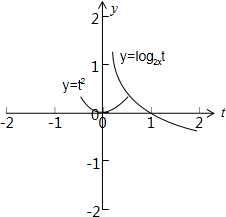 解:令y=t2,y=log2xt,不等式t2-log2xt<0对任意t∈(0,
解:令y=t2,y=log2xt,不等式t2-log2xt<0对任意t∈(0,
]恒成立,
即不等式t2<log2xt对任意t∈(0,
]恒成立,
就是t∈(0,
]时,函数的图象y=t2在y=log2xt的下方,如图:
可得
,
解得
<x<
,
故选A.
 解:令y=t2,y=log2xt,不等式t2-log2xt<0对任意t∈(0,
解:令y=t2,y=log2xt,不等式t2-log2xt<0对任意t∈(0,| 1 |
| 2 |
即不等式t2<log2xt对任意t∈(0,
| 1 |
| 2 |
就是t∈(0,
| 1 |
| 2 |
可得
|
解得
| 1 |
| 32 |
| 1 |
| 2 |
故选A.
点评:本题考查函数与方程的综合应用,函数的图象以及函数的恒成立,不等式的解法,考查转化思想与计算能力.

练习册系列答案
相关题目