题目内容
已知函数y=acos（2x+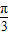
）+3，x∈[0，
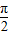]的最大值为4，则实数a的值为 ．
【答案】分析：由x∈[0，
]⇒2x+
∈[
，
]，利用余弦函数的单调性，结合题意即可求得实数a的值．
解答：解：∵x∈[0，
]，
∴2x+
∈[
，
]，
∴-1≤cos（2x+
）≤
，
当a＞0时，-a≤acos（2x+
）≤
a，
∵ymax=4，
∴
a+3=4，
∴a=2；
当a＜0时，
a≤acos（2x+
）≤-a
同理可得3-a=4，
∴a=-1．
综上所述，实数a的值为2或-1．
故答案为：2或-1．
点评：本题考查复合三角函数的单调性，考查转化与运算能力，属于中档题．
]⇒2x+∈[，]，利用余弦函数的单调性，结合题意即可求得实数a的值．解答：解：∵x∈[0，
]，∴2x+
∈[，]，∴-1≤cos（2x+
）≤，当a＞0时，-a≤acos（2x+
）≤a，∵ymax=4，
∴
a+3=4，∴a=2；
当a＜0时，
a≤acos（2x+）≤-a同理可得3-a=4，
∴a=-1．
综上所述，实数a的值为2或-1．
故答案为：2或-1．
点评：本题考查复合三角函数的单调性，考查转化与运算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2011•焦作一模）已知函数f（x）的图象过点（
已知函数y=Acos（