题目内容
已知函数f(x)=
,求:
(1)求出f[f(3)]的值;
(2)画出该函数的大致图象,并写出函数的单调区间.
|
(1)求出f[f(3)]的值;
(2)画出该函数的大致图象,并写出函数的单调区间.

(1)由于函数f(x)=
,可得 f(3)=-3+1=-2,故f([f(3)]=f(-2)=-9+2=-7.
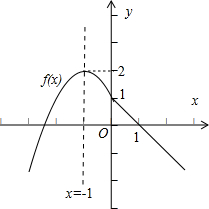
(2)函数f(x)的图象如图所示,显然函数的增区间为(-∞,-1),减区间为[-1,0)、[0,+∞).
|
(2)函数f(x)的图象如图所示,显然函数的增区间为(-∞,-1),减区间为[-1,0)、[0,+∞).


练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|