题目内容
已知![]() 是定义在R上的函数,其图象交x轴于A,B,C三点,若点B的坐标为(2,0),且
是定义在R上的函数,其图象交x轴于A,B,C三点,若点B的坐标为(2,0),且![]() 在
在![]() 和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)求c的值;
(2)在函数![]() 的图象上是否存在一点M(x0,y0),使得
的图象上是否存在一点M(x0,y0),使得![]() 在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,说明理由;
在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,说明理由;
⑴ c=0
⑵不存在点M(x0,y0),使得![]() 在点M的切线斜率为3b.
在点M的切线斜率为3b.
⑶ ![]()
解析:
⑴ ∵![]() 在
在![]() 和
和![]() 上有相反单调性,
上有相反单调性,
∴ x=0是![]() 的一个极值点,故
的一个极值点,故![]() ,
,
即![]() 有一个解为x=0,∴c=0
有一个解为x=0,∴c=0
⑵ ∵![]() 交x轴于点B(2,0)
交x轴于点B(2,0)
∴![]()
令![]() ,则
,则![]()
∵![]() 在
在![]() 和
和![]() 上有相反的单调性
上有相反的单调性
∴![]() , ∴
, ∴![]()
假设存在点M(x0,y0),使得![]() 在点M的切线斜率为3b,则
在点M的切线斜率为3b,则![]()
即 ![]()
∵ △=![]()
又![]() , ∴△<0
, ∴△<0
∴不存在点M(x0,y0),使得![]() 在点M的切线斜率为3b.
在点M的切线斜率为3b.
⑶ 依题意可令
![]()


∵![]() ,∴当
,∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
故![]()

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,在[0,2]上
,在[0,2]上 ,则
,则 ;[来源:Z§xx§k.Com]
;[来源:Z§xx§k.Com] 且
且 ;
; 在[-8,8]内恰有四个不同的根
在[-8,8]内恰有四个不同的根 ,则
,则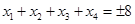 ;
;