Question

已知抛物线y²=2px(p＞0),A、B是抛物线上不重合的任意两点，F是抛物线的焦点，且,,O为坐标原点.

（1）若=，求点M的坐标；

（2）求动点M的轨迹方程.

Answer 1

解:设A、B的坐标分别为（x₁,y₁）、（x₂，y₂），则y₁²=2px₁,y₂²=2px,

∵=（x₁-,y₁）,=(x₂-,y₂),=0

∴

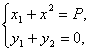
由y²₁+y²₂=2p(x₁+x₂)和y₁+y₂=0,得y₁²+y₂²=p²,x₁=x₂=.

∴y₁=p,y₂=-p;或y₁=-p,y₂=p.

∴=(x₁,y₁)+(x₂,y₂)=(x₁+x₂,y₁+y₂)=(p,0).

∴M的坐标为（p,0）.

(2)设动点M的坐标为（x,y），则由，得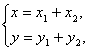

∵,

∴(x₁-)y₂-(x₂-)y₁=0,

∴(x₁y₂-x₂y₁)+(y₁-y₂)=0,

∴(y₁-y₂)=0,

∴(y₁-y₂)(y₁y₂+p²)=0,

∴y₁y₂+p²=0(y₁≠y₂).

∴y²=(y₁+y₂)²=y₁²+y₂²+2y₁y₂=2px-2p².

∴动点M的轨迹方程为y²=2p(x-p).