题目内容
函数f（x ）=αsin
+bcos
的一个零点为
，且f（
）＞f（
）＞0，对于下列结论：
①f（
）=0；②．f（x）≤f(
)；③．f(
) =f(
)；
④f（x）的单调减区间是[2k-
，2k+
] ，(k∈R)；
⑤f（x）的单调增区间是[4K+
，4K+
] ，(k∈Z)．
其中正确的有
| πx |
| 2 |
| πx |
| 2 |
| 1 |
| 3 |
| 17 |
| 15 |
| 11 |
| 6 |
①f（
| 7 |
| 3 |
| 4 |
| 3 |
| 13 |
| 12 |
| 19 |
| 12 |
④f（x）的单调减区间是[2k-
| 2 |
| 3 |
| 4 |
| 3 |
⑤f（x）的单调增区间是[4K+
| 10 |
| 3 |
| 16 |
| 3 |
其中正确的有
①②③⑤
①②③⑤
．（写出所有正确结论的编号）分析：利用辅助角公式化简函数为一个角的一个三角函数的形式，利用周期、零点求出辅助角，画出函数的图象，判断①②③④⑤，即可得到正确选项．
解答：解：函数f（x ）=asin
+bcos
=
sin（
+θ）其中tanθ=
，
因为函数f（x）的周期为4，一个零点为
，
所以
+θ=0，θ=-
，所以函数f（x ）=
sin（
-
），f（
）＞f（
）＞0，画出图象，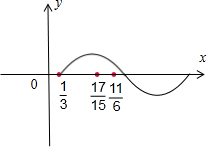
所以①正确；
②．f(
)=
sin(
-
) =
，所以f（x）≤f(
)；正确．
③f(
) =
sin
，
f(
)=
sin
=
sin
，所以f(
) =f(
)正确；
因为
-
∈[2kπ+
，2kπ+
]，k∈Z，
所以x∈[2k-
，2k+
] ，(k∈R)函数不是减函数，④不正确；
因为
-
∈[2kπ-
，2kπ+
]k∈Z，
所以x∈[4K+
，4K+
] ，(k∈Z)函数是增函数，⑤正确．
故答案为：①②③⑤．
| πx |
| 2 |
| πx |
| 2 |
| a2+b2 |
| πx |
| 2 |
| b |
| a |
因为函数f（x）的周期为4，一个零点为
| 1 |
| 3 |
所以
| π |
| 6 |
| π |
| 6 |
| a2+b2 |
| πx |
| 2 |
| π |
| 6 |
| 17 |
| 15 |
| 11 |
| 6 |
所以①正确；
②．f(
| 4 |
| 3 |
| a2+b2 |
| 2π |
| 3 |
| π |
| 6 |
| a2+b2 |
| 4 |
| 3 |
③f(
| 13 |
| 12 |
| a2+b2 |
| 9π |
| 24 |
f(
| 19 |
| 12 |
| a2+b2 |
| 15π |
| 24 |
| a2+b2 |
| 9π |
| 24 |
| 13 |
| 12 |
| 19 |
| 12 |
因为
| πx |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 3π |
| 2 |
所以x∈[2k-
| 2 |
| 3 |
| 4 |
| 3 |
因为
| πx |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
所以x∈[4K+
| 10 |
| 3 |
| 16 |
| 3 |
故答案为：①②③⑤．
点评：本题是中档题，考查三角函数的化简求值，函数的周期、单调性的应用，考查计算能力．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
选作题：考生任选一题作答，如果多做，则按所做的第一题计分．