Question

已知△ABC的三个顶点的极坐标分别为A(5,),B(5,),C(,),判断△ABC的形状，并求出它的面积.（提示：对于点M(ρ,θ)，当极径小于零时，此时M点在极角θ终边的反向延长线上，且OM=|ρ|）

Answer 1

思路分析：判断△ABC的形状，就需要计算三角形的边长或角，在本题中计算边长较为容易，不妨先计算边长.

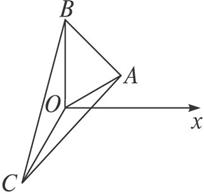
解：∵∠AOB=,∠BOC=,∠AOC=,

又∵|OA|=|OB|=5,|OC|=,

∴由余弦定理，得|AC|²=|OA|²+|OC|²-2|OA|·|OC|·cos∠AOC

=5²+()²-2×5×·cos=133.

∴|AC|=.同理,|BC|=.

∴|AC|=|BC|.∴△ABC为等腰三角形.

又|AB|=|OA|=|OB|=5,∴AB边上的高h=.

∴S_△ABC=×.