题目内容
【题目】设函数![]() 的定义域为
的定义域为![]() ,若存在闭区间
,若存在闭区间![]() ,使得函数
,使得函数![]() 满足:①
满足:①![]() 在
在![]() 上是单调函数;②
上是单调函数;②![]() 在
在![]() 上的值域是
上的值域是![]() ,则称区间
,则称区间![]() 是函数
是函数![]() 的“和谐区间”.下列结论错误的是( )
的“和谐区间”.下列结论错误的是( )
A. 函数![]() 存在“和谐区间”
存在“和谐区间”
B. 函数![]() 不存在“和谐区间”
不存在“和谐区间”
C. 函数![]() 存在“和谐区间”
存在“和谐区间”
D. 函数![]() (
(![]() 且
且![]() )不存在“和谐区间”
)不存在“和谐区间”
【答案】D
【解析】分析:利用函数单调性的判别方法,逐个选项检验函数是否存在单调区间。若函数![]() 在
在![]() 上的值域是
上的值域是![]() ,则方程
,则方程![]() 应该有两个根。
应该有两个根。
详解: 对于选项A,存在区间[0,2], ![]() 在
在![]() 上是单调增函数;②
上是单调增函数;②![]() 在
在![]() 上的值域是
上的值域是![]() ,故A正确;
,故A正确;
对于选项B,假设存在区间![]() ,函数
,函数![]() 在区间
在区间![]() 上为增函数,
上为增函数,
由![]() 在
在![]() 上的值域是
上的值域是![]() ,可得
,可得![]() ,
,
解得![]() ,这与
,这与![]() 矛盾,故假设错误,所以选项B正确;
矛盾,故假设错误,所以选项B正确;
对于选项C,由函数![]() ,可得
,可得
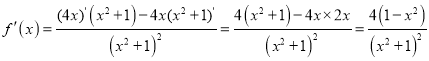 。
。
取区间![]() ,在此区间上
,在此区间上![]() ,
,
所以函数![]() 在区间
在区间![]() 上为增函数。
上为增函数。
因为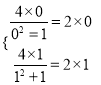 成立,
成立,
所以函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() .
.
所以选项C正确。
对于选项D,不妨设![]() ,则函数在定义域内为单调增函数。
,则函数在定义域内为单调增函数。
若存在“和谐区间”![]() ,则由
,则由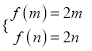 得
得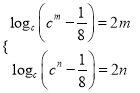 ,
,
所以![]() 是方程
是方程![]() 的两个根,
的两个根,
即![]() 是方程
是方程![]() 的两个根。
的两个根。
因为该方程有两个正根,所以存在“和谐区间”![]() 。所以选项D错。
。所以选项D错。
所以选D。

练习册系列答案
相关题目
【题目】已知函数![]() 的定义域为(0,+
的定义域为(0,+![]() ),若
),若![]() 在(0,+
在(0,+![]() )上为增函数,则称
)上为增函数,则称![]() 为“一阶比增函数”;若
为“一阶比增函数”;若![]() 在(0,+
在(0,+![]() )上为增函数,则称
)上为增函数,则称![]() 为”二阶比增函数”。我们把所有“一阶比增函数”组成的集合记为
为”二阶比增函数”。我们把所有“一阶比增函数”组成的集合记为![]() 1,所有“二阶比增函数”组成的集合记为
1,所有“二阶比增函数”组成的集合记为![]() 2。
2。
(1)已知函数![]() ,若
,若![]() ∈
∈![]() 1,求实数
1,求实数![]() 的取值范围,并证明你的结论;
的取值范围,并证明你的结论;
(2)已知0<a<b<c,![]() ∈
∈![]() 1且
1且![]() 的部分函数值由下表给出:
的部分函数值由下表给出:
|
|
|
|
|
|
|
| t | 4 |
求证:![]() ;
;
(3)定义集合![]() ,且存在常数k,使得任取x∈(0,+
,且存在常数k,使得任取x∈(0,+![]() ),
),![]() <k},请问:是否存在常数M,使得任意的
<k},请问:是否存在常数M,使得任意的![]() ∈
∈![]() ,任意的x∈(0,+
,任意的x∈(0,+![]() ),有
),有![]() <M成立?若存在,求出M的最小值;若不存在,说明理由。
<M成立?若存在,求出M的最小值;若不存在,说明理由。
