题目内容
已知一组数据x1, x2, x3, x4, x5的平均数为4，方差为
，那么另一组数据
3x1－1, 3x2－1, 3x3－1, 3x4－1, 3x5－1的平均数与方差分别为_________ 、_________ .
平均数11，方差3（本题答对一空得3分，全对得5分）
解析试题分析： 因为：∵据x1，x2，x3，x4，x5的平均数是4，所以有
，那么由方差为
可知3x1－1, 3x2－1, 3x3－1, 3x4－1, 3x5－1的平均数为
，而方差则为
，故答案为平均数11，方差3
考点：本题主要考查了平均数的计算公式和方差的定义的运用。
点评：解决该试题的关键是理解一般地设n个数据，x1，x2，…xn的平均数为
，
它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
练习册系列答案
相关题目
某工厂的某种型号的机器的使用年限
和所支出的维修费用
(万元)有下表的统计资料：
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
根据上表可得回归方程
，据此模型估计，该型号机器使用年限为10年时维修费用约 万元（结果保留两位小数）． 
人，女运动员
人，若用分层抽样的方法从该队的全体运动员中抽取一个容量为
的样本，则抽取男运动员的人数为_______．
构成一组新数据，则这组新数据的平均数是 
，方差是
，则原来一组数的方差为______．
辆汽车通过某一段公路时的时速的频率分布直方图如图1所示，则 时速在
的汽车大约有_________辆.
某服装商场为了了解毛衣的月销售量
（件）与月平均气温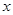
（℃）之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：
| 月平均气温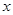（℃） | 17 | 13 | 8 | 2 |
| 月销售量（件） | 24 | 33 | 40 | 55 |
中的
，气象部门预测下个月的平均气温约为6℃，据此估计，该商场下月毛衣的销售量约为 件。 