题目内容
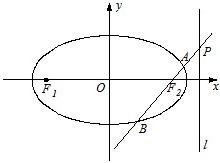 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)求△F1AB的面积S的取值范围;
(Ⅲ)设
| AF2 |
| F2B |
| AP |
| PB |
分析:(1)根据离心率求得a和c的关系,进而根据F2到椭圆C的右准线l的距离为1和a2=b2+c2求得a和b,椭圆的方程可得.
(2)可设动点P的坐标为(2,m),求得焦点坐标,进而可得直线PF2的方程与椭圆方程联立消去y,设A,B两点的坐标分别为(x1,y1),(x2,y2),根据伟大定理可表示出x1+x2和x1x2,进而表示出|AB|和点F1到直线PF2的距离,进而可得△F1AB的面积S的表达式,根据m确定S的取值范围.
(3)根据
=λ
,
=μ
,可求得λ和μ的表达式,进而把x1+x2和x1x2代入λ+μ中求得λ+μ=0,原式得证.
(2)可设动点P的坐标为(2,m),求得焦点坐标,进而可得直线PF2的方程与椭圆方程联立消去y,设A,B两点的坐标分别为(x1,y1),(x2,y2),根据伟大定理可表示出x1+x2和x1x2,进而表示出|AB|和点F1到直线PF2的距离,进而可得△F1AB的面积S的表达式,根据m确定S的取值范围.
(3)根据
| AF2 |
| F2B |
| AP |
| PB |
解答: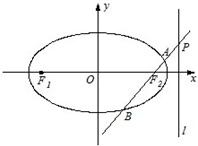 解:
解:
(Ⅰ)由题意得
,
解得a=
,b=1,c=1,
所以椭圆C的方程为
+y2=1.
(Ⅱ)因为右准线l的方程为x=
=2,
所以可设动点P的坐标为(2,m),由(Ⅰ)知焦点F1,F2的坐标分别(-1,0),(1,0),
所以直线PF2的方程为y=m(x-1).
设A,B两点的坐标分别为(x1,y1),(x2,y2),
由
得(1+2m2)x2-4m2x+2m2-2=0,
于是x1+x2=
,x1x2=
.
所以|AB|=
=
.
点F1到直线PF2的距离d=
,
所以△F1AB的面积S=
|AB|d=
,S2=
=
=2-
,
由题知m∈R且m≠0,于是0<S<
,
故△F1AB的面积S的取值范围是(0,
).
(Ⅲ)由(Ⅱ)及
=λ
,
=μ
,得(1-x1,-y1)=λ(x2-1,y2),(2-x1,m-y1)=μ(x2-2,y2-m),
于是λ=
,μ=
,
所以λ+μ=
+
=
.
因为3(x1+x2)-2x1x2-4=
-
-4=0,
所以λ+μ=0,即λ+μ为定值0.
 解:
解:(Ⅰ)由题意得
|
解得a=
| 2 |
所以椭圆C的方程为
| x2 |
| 2 |
(Ⅱ)因为右准线l的方程为x=
| a2 |
| c |
所以可设动点P的坐标为(2,m),由(Ⅰ)知焦点F1,F2的坐标分别(-1,0),(1,0),
所以直线PF2的方程为y=m(x-1).
设A,B两点的坐标分别为(x1,y1),(x2,y2),
由
|
于是x1+x2=
| 4m2 |
| 1+2m2 |
| 2m2-2 |
| 1+2m2 |
所以|AB|=
| (x1-x2)2+(y1-y2)2 |
2
| ||
| 1+2m2 |
点F1到直线PF2的距离d=
| 2|m| | ||
|
所以△F1AB的面积S=
| 1 |
| 2 |
2
| ||||
| 1+2m2 |
| 8m2(1+m2) |
| (1+2m2)2 |
| 2(1+2m2)2-2 |
| (1+2m2)2 |
| 2 |
| (1+2m2)2 |
由题知m∈R且m≠0,于是0<S<
| 2 |
故△F1AB的面积S的取值范围是(0,
| 2 |
(Ⅲ)由(Ⅱ)及
| AF2 |
| F2B |
| AP |
| PB |
于是λ=
| 1-x1 |
| x2-1 |
| 2-x1 |
| x2-2 |
所以λ+μ=
| 1-x1 |
| x2-1 |
| 2-x1 |
| x2-2 |
| 3(x1+x2)-2x1x2-4 |
| (x2-1)(x2-2) |
因为3(x1+x2)-2x1x2-4=
| 12m2 |
| 1+2m2 |
| 4m2-4 |
| 1+2m2 |
所以λ+μ=0,即λ+μ为定值0.
点评:本题主要考查了椭圆的标准方程.当涉及直线与圆锥曲线的关系时,常需要把直线方程和圆锥曲线方程联立,根据伟大定理找到解决问题的途径.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目