题目内容
已知数列![]() ,其前n项和
,其前n项和![]() 满足
满足![]() (
(![]() 是大于0的常数),且
是大于0的常数),且![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
解:(Ⅰ)由![]() 得
得![]() ,
,![]() .
.
![]() ,
,![]() …………………………………………………………3分
…………………………………………………………3分
(Ⅱ)由![]() 整理得:
整理得:![]()
所以数列![]() 是以
是以![]() 为首项,2 为公比的等比数列.…………………………5分
为首项,2 为公比的等比数列.…………………………5分
![]() ………………………………………………………………6分
………………………………………………………………6分
![]() .………………………………………………………………7分
.………………………………………………………………7分
因为当![]() 时,
时,![]() 满足
满足![]() ,
,![]() ………………………………………8分
………………………………………8分
(Ⅲ)![]() ①
①
![]() ②
②
①-②得:![]() .
.
则![]() ,……………………………………………………………………11分
,……………………………………………………………………11分
![]() .………………………………12分
.………………………………12分
∴当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() .
.
即当![]() 或
或![]() 时,
时,![]() .………………………………………………13分
.………………………………………………13分
当![]() 时,
时,![]() .…………………………………………………………14分
.…………………………………………………………14分

练习册系列答案
相关题目
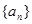 ,其前n项和
,其前n项和 ,满足
,满足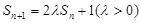 ,且
,且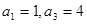 。
。
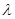 的值;
的值; ;
;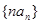 的前
的前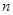 项和为
项和为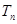 ,试比较
,试比较 与
与 ,其前n项和
,其前n项和 = 。
= 。