题目内容
已知实数x,y满足x2+y2-2x+4y+4=0,则x-2y的最小值为________.
5-
分析:把x2+y2-2x+4y+4=0配方可知表示圆,用三角换元的方式可把要求的式子化为三角函数来求解,可得答案.
解答:把x2+y2-2x+4y+4=0配方得:(x-1)2+(y+2)2=1,
显然是一个圆的方程,设x-1=cosα,y+2=sinα,
则x-2y=1+cosα+4-2sinα= cos(α+∅)+5,其中tan∅=2
cos(α+∅)+5,其中tan∅=2
由余弦函数的值域可知 cos(α+∅)∈[
cos(α+∅)∈[ ,
, ],
],
故 cos(α+∅)+5∈[5
cos(α+∅)+5∈[5 ,
, +5],即最小值为:
+5],即最小值为: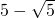
故答案为: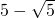
点评:本题为最值的求解,把问题转化为三角函数的运算是解决问题的关键,属基础题.

分析:把x2+y2-2x+4y+4=0配方可知表示圆,用三角换元的方式可把要求的式子化为三角函数来求解,可得答案.
解答:把x2+y2-2x+4y+4=0配方得:(x-1)2+(y+2)2=1,
显然是一个圆的方程,设x-1=cosα,y+2=sinα,
则x-2y=1+cosα+4-2sinα=
 cos(α+∅)+5,其中tan∅=2
cos(α+∅)+5,其中tan∅=2由余弦函数的值域可知
 cos(α+∅)∈[
cos(α+∅)∈[ ,
, ],
],故
 cos(α+∅)+5∈[5
cos(α+∅)+5∈[5 ,
, +5],即最小值为:
+5],即最小值为: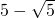
故答案为:
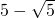
点评:本题为最值的求解,把问题转化为三角函数的运算是解决问题的关键,属基础题.

练习册系列答案
相关题目
已知实数x,y满足
-
=1(a>0,b>0),则下列不等式中恒成立的是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、|y|<
| ||
B、y>-
| ||
C、|y|>-
| ||
D、y<
|