题目内容
已知定义在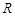 上的函数
上的函数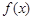 满足
满足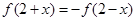 ,当
,当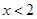 时,
时,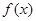 单调递增,若
单调递增,若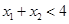 且
且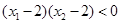 ,则
,则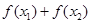 的值( )
的值( )
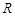 上的函数
上的函数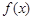 满足
满足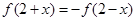 ,当
,当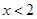 时,
时,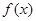 单调递增,若
单调递增,若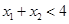 且
且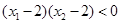 ,则
,则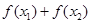 的值( )
的值( )| A.可能为0 | B.恒大于0 | C.恒小于0 | D.可正可负 |
C
试题分析:根据题意,由于定义在
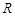 上的函数
上的函数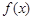 满足
满足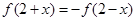 ,则说明函数关于(2,0)呈对称中心图象,那么当
,则说明函数关于(2,0)呈对称中心图象,那么当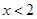 时,
时,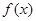 单调递增,x>2,函数递减,那么
单调递增,x>2,函数递减,那么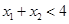 且
且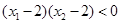 ,则可知
,则可知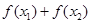 恒小于0,故可知选C.
恒小于0,故可知选C.点评:主要是考查了函数的单调性的运用,属于基础题。

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
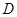 的函数
的函数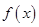 ,其导函数为
,其导函数为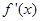 .若对
.若对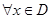 ,均有
,均有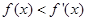 ,则称函数
,则称函数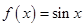 ,试判断
,试判断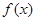 是否为其定义域上的梦想函数,并说明理由;
是否为其定义域上的梦想函数,并说明理由;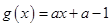 (
(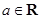 ,
,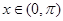 )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求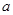 的取值范围;
的取值范围;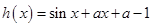 (
(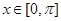 )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求 满足
满足 ,且当
,且当  时,
时, 等于 ( )
等于 ( )



 上的奇函数
上的奇函数 是减函数,且
是减函数,且 ,则
,则 的取值范围是( )
的取值范围是( ) ,3)
,3)  )
) ,
, 满足
满足 ,
, ,若
,若 且
且 ,则
,则 =____.
=____.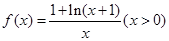 .
.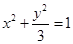 在
在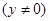
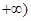 上单调性并证明你的结论;
上单调性并证明你的结论;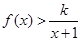 恒成立, 求整数
恒成立, 求整数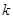 的最大值;
的最大值;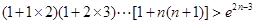 .
.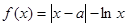
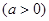 .
.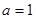 ,求
,求 的单调区间及
的单调区间及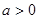 ,求
,求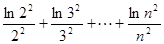 与
与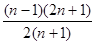 的大小
的大小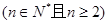 ,并证明你的结论.
,并证明你的结论.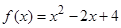 的单调减区间是 .
的单调减区间是 .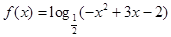 的单调递减区间为
的单调递减区间为