Question

【题目】选修4-4：坐标系与参数方程

在直角坐标系中，直线的参数方程为（为参数），直线的参数方程为（为参数），设与的交点为，当变化时， 的轨迹为曲线.

（1）写出的普遍方程及参数方程；

（2）以坐标原点为极点， 轴正半轴为极轴建立极坐标系，设曲线的极坐标方程为， 为曲线上的动点，求点到的距离的最小值.

Answer 1

【答案】(1)详见解析;(2) .

【解析】试题分析：先把两条直线的参数方程化为普通方程，然后利用两条直线的方程削去参数k，得出点P的轨迹方程，再把椭圆的直角坐标方程改为参数方程；把曲线的极坐标方程化为直角坐标方程，得到直线的方程，利用椭圆的参数方程巧设点Q的坐标，写出点到直线的距离，利用三角函数求最值.

试题解析：

（Ⅰ）将参数方程转化为一般方程

，①

，②

①×②消可得： ．

即的轨迹方程为． 的普通方程为．

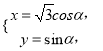的参数方程为（为参数）．

（Ⅱ）由曲线： 得： ，

即曲线的直角坐标方程为：

由（Ⅰ）知曲线与直线无公共点，

曲线上的点到直线的距离为

，

所以当时， 的最小值为．