题目内容
已知直线l：x-y-1=0，l1：2x-y-2=0．则两直线夹角的余弦值为 ．
【答案】分析：设两条直线的夹角为α，根据两条直线所成角的公式，算出tanα=
．再由同角三角函数的基本关系，算出cosα=
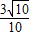，即得本题答案．
解答：解：直线l、l1的斜率分别为k=1，k1=2
设两条直线的夹角为α，则tanα=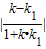
=
∵α为锐角，∴cosα=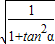
=
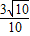
故答案为：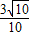
点评：本题给出两条直线，求它们夹角的余弦之值．着重考查了直线的斜率和两条直线的夹角公式等知识，属于基础题．
．再由同角三角函数的基本关系，算出cosα=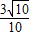，即得本题答案．解答：解：直线l、l1的斜率分别为k=1，k1=2
设两条直线的夹角为α，则tanα=
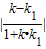=∵α为锐角，∴cosα=
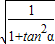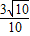
=故答案为：
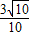
点评：本题给出两条直线，求它们夹角的余弦之值．着重考查了直线的斜率和两条直线的夹角公式等知识，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目