题目内容
设f(x)对一切自然数有定义,且①f(x)是整数;②f(2)=2;③f(m·n)=f(m)·f(n)对一切自然数成立;④当m>n时,有f(m)>f(n),试证:f(n)=n.
证明:(1)由于2=f(2)=f(1·2)=f(1)·f(2)=
(2)设n≤k时,有f(k)=k.
当n=k+1时,若k+1为偶数,则k+1=2i(i∈N且i≤k),
∴f(k+1)=f(2i)=f(2)·f(i)=2i=k+1;若k+1为奇数,则k+2为偶数,即k+2=2(i+1)(i∈N且i+1≤k).
∴f(k+2)=f[2(i+1)]=f(2)·f(i+1)=2(i+1)=k+2.
由于k<k+1<k+2,
∴f(k)<f(k+1)<f(k+2)且f(n)为整数,故f(k+1)=k+1,即当n=k+1时结论成立.
由(1)(2),知对于n∈N都有f(n)=n.

练习册系列答案
相关题目

 +
+ ,g(x)=
,g(x)=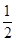 ln(2ex)(其中e为自然对数的底数)
ln(2ex)(其中e为自然对数的底数)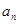 }中,a1=1,
}中,a1=1,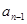 )(n≥2),求证:
)(n≥2),求证: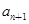 <
<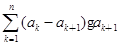 <
<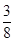 .
.