题目内容
定义:若数列{An}满足 ,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
(1)证明:数列{2an+1}是“平方递推数列”,且数列{lg(2an+1)}为等比数列.
(2)设(1)中“平方递推数列”的前n项之积为Tn,即Tn=(2a1+1)(2a2+1)…(2an+1),求数列{an}的通项及Tn关于n的表达式.
(3)记 ,求数列{bn}的前n项之和Sn,并求使Sn>2011的n的最小值.
,求数列{bn}的前n项之和Sn,并求使Sn>2011的n的最小值.
(1)证明:由条件得: ,
,
∴ ,
,
∴{2an+1}是“平方递推数列”. …(4分)
由lg(2an+1+1)=2lg(2an+1),
∴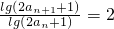 ,
,
∴{lg(2an+1)}为等比数列. …(6分)
(2)解:∵lg(2a1+1)=lg5,∴ ,
,
∴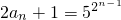
∴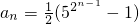 . …(8分)
. …(8分)
∵ ,
,
∴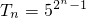 . …(10分)
. …(10分)
(3)解: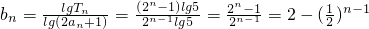 ,…(12分)
,…(12分)
∴
=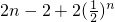 . …(14分)
. …(14分)
由Sn>2011,得 ,
,
当n≤1006时, ,当n≥1007时,
,当n≥1007时, ,
,
因此n的最小值为1007. …(16分)
分析:(1)根据点(an,an+1)在函数f(x)=2x2+2x的图象上,可得数列递推式,再进行变形,利用定义即可得到结论;
(2)先确定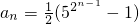 ,再利用对数运算,即可求得Tn关于n的表达式;
,再利用对数运算,即可求得Tn关于n的表达式;
(3)因为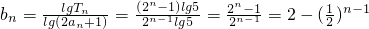 ,所以Sn=
,所以Sn=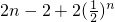 ,再根据Sn>2011,即可求得n的最小值.
,再根据Sn>2011,即可求得n的最小值.
点评:本题考查数列的应用,考查新定义,考查数列的通项与求和,解题的关键是理解新定义,确定数列的通项.
 ,
,∴
 ,
,∴{2an+1}是“平方递推数列”. …(4分)
由lg(2an+1+1)=2lg(2an+1),
∴
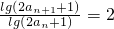 ,
,∴{lg(2an+1)}为等比数列. …(6分)
(2)解:∵lg(2a1+1)=lg5,∴
 ,
,∴
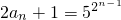
∴
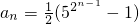 . …(8分)
. …(8分)∵
 ,
,∴
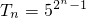 . …(10分)
. …(10分)(3)解:
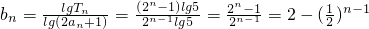 ,…(12分)
,…(12分)∴

=
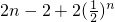 . …(14分)
. …(14分)由Sn>2011,得
 ,
,当n≤1006时,
 ,当n≥1007时,
,当n≥1007时, ,
,因此n的最小值为1007. …(16分)
分析:(1)根据点(an,an+1)在函数f(x)=2x2+2x的图象上,可得数列递推式,再进行变形,利用定义即可得到结论;
(2)先确定
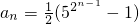 ,再利用对数运算,即可求得Tn关于n的表达式;
,再利用对数运算,即可求得Tn关于n的表达式;(3)因为
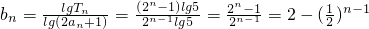 ,所以Sn=
,所以Sn=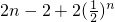 ,再根据Sn>2011,即可求得n的最小值.
,再根据Sn>2011,即可求得n的最小值.点评:本题考查数列的应用,考查新定义,考查数列的通项与求和,解题的关键是理解新定义,确定数列的通项.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目