题目内容
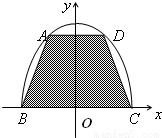
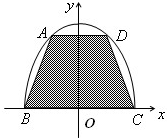 如图,用一块形状为半椭圆x2+
如图,用一块形状为半椭圆x2+| y2 |
| 4 |
| 1 |
| S |
2
| ||
| 9 |
2
| ||
| 9 |
分析:设D点坐标为(x,y)(x>0),由点D在椭圆上知x2+
=1(y≥0),得y2=4(1-x2),用x,y表示出等腰梯形ABCD的面积为S=
(|AD|+|BC|)|y|=
(2x+2)•y=(x+1)•y,将y2=4(1-x2)代入得S2=(x+1)2•y2=(x+1)2•4(1-x2)=4(-x4-2x3+2x+1),利用导数求此函数的最值.
| y2 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设D点坐标为(x,y)(x>0),由点D在椭圆上知x2+
=1(y≥0),得y2=4(1-x2)
∴等腰梯形ABCD的面积为S=
(|AD|+|BC|)|y|=
(2x+2)•y=(x+1)•y (2分)
∴S2=(x+1)2•y2=(x+1)2•4(1-x2)=4(-x4-2x3+2x+1)=-4x4-8x3+8x+4(0<x<1)
(S2)′=4(-4x3-6x2+2),
令(S2)′=0,得2x3+3x2-1=0,即(x+1)2(2x-1)=0,
∵0<x<1,∴x=
,
又当0<x<
时,(S2)′>0;当
<x<1时,(S2)′<0,
∴在区间(0,1)上,S2有唯一的极大值点x=
,
∴当x=
时,S2有最大值为
;即当x=
时,S有最大值为
,
∴
的最小值为
=
故答案为:
| y2 |
| 4 |
∴等腰梯形ABCD的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
∴S2=(x+1)2•y2=(x+1)2•4(1-x2)=4(-x4-2x3+2x+1)=-4x4-8x3+8x+4(0<x<1)
(S2)′=4(-4x3-6x2+2),
令(S2)′=0,得2x3+3x2-1=0,即(x+1)2(2x-1)=0,
∵0<x<1,∴x=
| 1 |
| 2 |
又当0<x<
| 1 |
| 2 |
| 1 |
| 2 |
∴在区间(0,1)上,S2有唯一的极大值点x=
| 1 |
| 2 |
∴当x=
| 1 |
| 2 |
| 27 |
| 4 |
| 1 |
| 2 |
3
| ||
| 2 |
∴
| 1 |
| S |
| 1 | ||||
|
2
| ||
| 9 |
故答案为:
2
| ||
| 9 |
点评:本题考查椭圆方程的应用,解题的关键是根据椭圆的方程消元,将面积表示成x的函数,再利用导数研究此函数的最值,此题运算量很大,属中档题.

练习册系列答案
相关题目
 如图,用一块形状为半椭圆
如图,用一块形状为半椭圆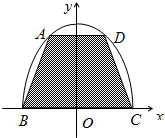 如图,用一块形状为半椭圆
如图,用一块形状为半椭圆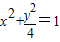 (y≥0)的铁皮截取一个以短轴BC为底的等腰梯形ABCD,记所得等腰梯形的面积为S,则
(y≥0)的铁皮截取一个以短轴BC为底的等腰梯形ABCD,记所得等腰梯形的面积为S,则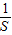 的最小值是 .
的最小值是 .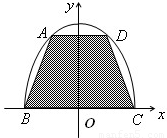
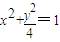 (y≥0)的铁皮截取一个以短轴BC为底的等腰梯形ABCD,问:怎样截才能使所得等腰梯形ABCD的面积最大?
(y≥0)的铁皮截取一个以短轴BC为底的等腰梯形ABCD,问:怎样截才能使所得等腰梯形ABCD的面积最大?