题目内容
已知（b-c）logmx+（c-a）logmy+（a-b）logmz=0.（1）设a，b，c依次成等差数列，且公差不为0.
求证：x，y，z成等比数列.
（2）设正数x，y，z依次成等比数列，且公比不为1.求证：a，b，c成等差数列.
解：（1）∵a，b，c成等差数列，且公差d≠0， ∴b-c=a-b=-d，c-a=2d. 代入已知条件，得 -d（logmx-2logmy+logmz）=0. ∴logmx-2logmy+logmz=0. logmx+logmz=2logmy，即logmxz=logmy2. ∴y2=xz. 又x，y，z都是正数，∴x，y，z成等比数列. （2）∵x，y，z成等比数列，且公比q≠1， ∴y=xq，z=xq2.把它们都代入已知条件，得 （b-c）logmx+（c-a）logmxq+（a-b）logmxq2=0. 整理，得（c+a-2b）logmq=0. 其中q≠1，∴logmq≠0，∴c+a-2b=0， 即2b=a+c. 因此，a，b，c成等差数列.
练习册系列答案
西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
萌齐小升初强化模拟训练系列答案
相关题目
(3x2－ax＋5)在[－1，＋∞)上是减函数，则实数a的取值范围是( )
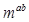<1,则m的取值范围是（ ）
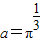，b=logπ3，
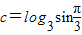，则a，b，c大小关系为（ ）
，b=logπ3，
，则a，b，c大小关系为（ ）
，b=logπ3，
，则a，b，c大小关系为（ ）