题目内容
已知 的夹角为arctan2,则实数m的值为( )
的夹角为arctan2,则实数m的值为( )A.

B.

C.-7或9
D.1或-11
【答案】分析:利用两个向量的数量积公式求出 =4-m,再利用两个向量的数量积的定义求出
=4-m,再利用两个向量的数量积的定义求出 =
= ,由 4-m=
,由 4-m= ,解方程求得m的值.
,解方程求得m的值.
解答:解:令arctan2=θ,则θ为锐角,且tanθ=2,cosθ= ,sinθ=
,sinθ= .
.
又 ,∴
,∴ ,
, =1.
=1.
∴ =
= =5+m-1-2m=4-m…①
=5+m-1-2m=4-m…①
又 =(1-m,2+m),
=(1-m,2+m), =(2,1),∴
=(2,1),∴ =
= =
= ,
, =
= .
.
 =
= ×
× cosθ=
cosθ= …②
…②
由①②可得 4-m= ,∴m=1或 m=-11.
,∴m=1或 m=-11.
故选D.
点评:本题主要考查两个向量的数量积的定义,数量积公式的应用,求向量的模的方法,两个向量坐标形式的运算,两个向量夹角公式的应用,属于中档题.
 =4-m,再利用两个向量的数量积的定义求出
=4-m,再利用两个向量的数量积的定义求出 =
= ,由 4-m=
,由 4-m= ,解方程求得m的值.
,解方程求得m的值.解答:解:令arctan2=θ,则θ为锐角,且tanθ=2,cosθ=
 ,sinθ=
,sinθ= .
.又
 ,∴
,∴ ,
, =1.
=1. ∴
 =
= =5+m-1-2m=4-m…①
=5+m-1-2m=4-m…①又
 =(1-m,2+m),
=(1-m,2+m), =(2,1),∴
=(2,1),∴ =
= =
= ,
, =
= .
. =
= ×
× cosθ=
cosθ= …②
…②由①②可得 4-m=
 ,∴m=1或 m=-11.
,∴m=1或 m=-11.故选D.
点评:本题主要考查两个向量的数量积的定义,数量积公式的应用,求向量的模的方法,两个向量坐标形式的运算,两个向量夹角公式的应用,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目

 的夹角为120º,则
的夹角为120º,则
 的夹角为
的夹角为 则
则 在
在 上的投影为
上的投影为

 ,
, 的夹角为60o,
的夹角为60o, ,
, ,当实数
,当实数 为何值时,
为何值时, ∥
∥ ;
⑵
;
⑵ 。
。 的夹角为
的夹角为 ,则实数
,则实数 的值为 .
的值为 .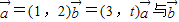 的夹角为锐角,则t的取值范围为 .
的夹角为锐角,则t的取值范围为 .