题目内容
若点M是 ABC所在平面内一点,且满足:
ABC所在平面内一点,且满足: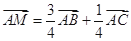 .
.
(1)求 ABM与
ABM与 ABC的面积之比.
ABC的面积之比.
(2)若N为AB中点,AM与CN交于点O,设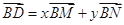 ,求
,求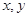 的值.
的值.
(1)1:4;(2) .
.
解析试题分析:(1)令 ,然后利用三角形法则用
,然后利用三角形法则用 表示
表示 ,求出
,求出 ,即求出面积比值;
,即求出面积比值;
(2)利用三角形法则和平面向量基本定理表示,由

 ,由O、M、A三点共线及O、N、C三点共线,解出
,由O、M、A三点共线及O、N、C三点共线,解出
试题解析:解(1)由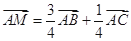 可知M、B、C三点共线
可知M、B、C三点共线
如图令


 即面积之比为1:4
即面积之比为1:4
(2)由


由O、M、A三点共线及O、N、C三点共线
考点:1.三角形法则;2.平面向量基本定理.

练习册系列答案
相关题目
 的方向向量为
的方向向量为 ,且过点
,且过点 ,将直线
,将直线 绕着它与x轴的交点B按逆时针方向旋转一个锐角
绕着它与x轴的交点B按逆时针方向旋转一个锐角 得到直线
得到直线 ,直线
,直线 :
: .(k
.(k R).
R). 的终边分别与单位圆交于A、B两点。
的终边分别与单位圆交于A、B两点。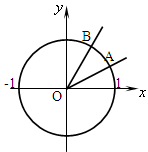
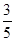 ,点B的横坐标为
,点B的横坐标为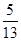 ,求
,求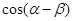 ;
;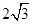 ,-2),
,-2),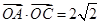 ,求
,求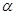
 ,
, .
.  ,求实数
,求实数 的值;
的值; 为直角三角形,求实数
为直角三角形,求实数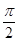 (k∈Z).
(k∈Z). 按下列条件求
按下列条件求 值。
值。 ; (2)
; (2) .
. ,
, ,
, ·
· =
= ,
, ∈(0,
∈(0, ).
). 及
及 ,
, 的值;
的值; ,求
,求 的最小正周期和图象的对称中心坐标;
的最小正周期和图象的对称中心坐标; 上的值域.
上的值域. ABC的外接圆的圆心为O,半径为1,
ABC的外接圆的圆心为O,半径为1, ,且
,且 ,则向量
,则向量 在向量
在向量 方向上的投影为_______。
方向上的投影为_______。