题目内容
已知集合A={x|x=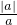 +
+ ,ab≠0,a∈R,b∈R}
,ab≠0,a∈R,b∈R}
(1)用列举法写出集合A;
(2)若B={x|mx-1=0,m∈R},且B⊆A,求m的值.
解:(1)①当a>0、b>0时,x= =2;
=2;
②当a<0、b<0时,x= =-2;
=-2;
③当ab<0时,x=-1+1=0.
综上①②③可知:A={0,-2,2}.
(2)①若m=0时,则B=∅,满足B⊆A,适合题意;
②当m≠0时,B={ }.
}.
∵B⊆A,∴B={-2}或{2}.
∴ =-2或2.解得m=
=-2或2.解得m= 或
或 .
.
综上可知:m=0, 或
或 .
.
分析:(1)通过对a、b的正负分类讨论即可求出A;
(2)利用B⊆A的关系即可求出m的值.
点评:熟练掌握分类讨论思想方法和集合间的关系是解题的关键.
 =2;
=2;②当a<0、b<0时,x=
 =-2;
=-2;③当ab<0时,x=-1+1=0.
综上①②③可知:A={0,-2,2}.
(2)①若m=0时,则B=∅,满足B⊆A,适合题意;
②当m≠0时,B={
 }.
}.∵B⊆A,∴B={-2}或{2}.
∴
 =-2或2.解得m=
=-2或2.解得m= 或
或 .
.综上可知:m=0,
 或
或 .
.分析:(1)通过对a、b的正负分类讨论即可求出A;
(2)利用B⊆A的关系即可求出m的值.
点评:熟练掌握分类讨论思想方法和集合间的关系是解题的关键.

练习册系列答案
相关题目