题目内容

给定椭圆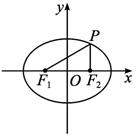+=1(a＞b＞0).椭圆上是否存在点P.使得点P对左、右焦点F1，F2所成的角∠F1PF2最大？若存在求点P的坐标；若不存在，说理由.

解：设|PF1|=r1，|PF2|=r2.

    则cos∠F1PF2==

==-1=-1.

∵r1r2≤()2=a2,当且仅当r1=r2时取等号，

∴cos∠F1PF2≥-1,

∴∠F1PF2≤arccos.

    故∠F1PF2存在最大值arccos.此时P(0,±b).

练习册系列答案
相关题目
在给定椭圆中，过焦点且垂直于长轴的弦长为
2
，焦点到相应准线的距离为1，则该椭圆的离心率为（　　）
A、
2
B、
2
2
C、
1
2
D、
2
4
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
2
2
，椭圆C上的点到左焦点F距离的最小值与最大值之积为1．
（1）求椭圆C的方程；
（2）直线l过椭圆C内一点M（m，0），与椭圆C交于P、Q两点．对给定的m值，若存在直线l及直线母x=-2上的点N，使得△PNQ的垂心恰为点F，求m的取值范围．
给定椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0），称圆心在坐标原点O，半径为
a2+b2
的圆是椭圆C的“伴随圆”． 若椭圆C的一个焦点为F2（
2
，0），其短轴上的一个端点到F2距离为
3
．
（Ⅰ）求椭圆C及其“伴随圆”的方程；
（Ⅱ）若过点P（0，m）（m＜0）的直线l与椭圆C只有一个公共点，且l截椭圆C的“伴随圆”所得的弦长为2
2
，求m的值．
若给定椭圆C：ax2+by2=1（a＞0，b＞0，a≠b）和点N（x0，y0），则称直线l：ax0x+by0y=1为椭圆C的“伴随直线”．
（1）若N（x0，y0）在椭圆C上，判断椭圆C与它的“伴随直线”的位置关系（当直线与椭圆的交点个数为0个、1个、2个时，分别称直线与椭圆相离、相切、相交），并说明理由；
（2）命题：“若点N（x0，y0）在椭圆C的外部，则直线l与椭圆C必相交．”写出这个命题的逆命题，判断此逆命题的真假，说明理由；
（3）若N（x0，y0）在椭圆C的内部，过N点任意作一条直线，交椭圆C于A、B，交l于M点（异于A、B），设
MA
=λ1
AN
，
MB
=λ2
BN
，问λ1+λ2是否为定值？说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网