题目内容
已知圆心为C的圆经过点A(-1,1)和B(-2,-2),且圆心在直线L:x+y-1=0上,求圆心为C的圆的标准方程.
(x-3)²+(y+2)²=25
解析试题分析:解:设圆的标准方程为(x-a)²+(y-b)²=r²,圆心C(a,b),半径r
依题意和圆经过点A(-1,1),点B(-2,-2)且圆心C(a,b)在直线L:x+y-1=0上
则有 (-1-a)²+(1-b)²=r² (1)
(-2-a)²+(-2-b)²=r² (2)
a+b="1" (3)
得 a=3,b=-2 r²="12+13" ="25"
圆心为C(3,-2)的圆的标准方程(x-3)²+(y+2)²=25
考点:圆的标准方程
点评:要得到圆的标准方程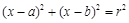 ,需求出圆的圆心
,需求出圆的圆心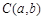 和半径
和半径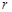 。
。

练习册系列答案
相关题目