Question

从集合{-1，-2，-3，-4，0，1，2，3，4，5}中，选出5个数组成子集，使得这5个数中的任何两个数之和不等于1，则取出这样的子集的概率为________．

Answer 1

分析：先求出试验的结果共有C₁₀5，记：“这5个数中的任何两个数之和不等于1”为事件A，通过找事件A的对立事件 ，代入古典概率的计算公式及 ，进行计算
解答：从集合{-1，-2，-3，-4，0，1，2，3，4，5}中，随机选出5个数组成子集，共有C₁₀5种取法，即可组成C₁₀5个子集，
记“这5个数中的任何两个数之和不等于1”为事件A，
而两数之和为1的数组分别为（-1，2），（-2，3），（-3，4）（-4，5），（0，1），
包含的结果有①只有有一组数的和为1，有C₅1C₄3C₂1C₂1C₂1=160种结果
②有两组数之和为1，有C₅2•C₆1=60种，
则A包含的结果共有220种，
由古典概率的计算公式可得P（A）=1-P（ ）=
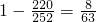
故答案为：．
点评：本题主要考查了古典概率的计算及利用对了事件求解概率的运用，当直接求解一个事件的概率比较困难或正面情况比较多时，往往找其反面即对立事件的个数，利用公式P（A）=1-P（ ），进行计算．