题目内容
【题目】若函数
， 
， 
， 
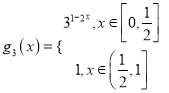在等差数列
中, 
，
用
表示数列
的前2018项的和，则（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】等差数列{an}中,a1=0,a2019=1,可知该数列为递增数列,且a1010=
,a505<
,a506>
，
对于g1(x)=2x,该函数在[0,1]上单调递增,于是有g1(an+1)g1(an)>0，
于是bn=g1(an+1)g1(an)，
∴P1=g1(a2019)g1(a1)=21=1，
对于g2(x),该函数在
上递增，在区间
上单调递减，
于是P2=g2(a1010)g2(a1)+g2(a1010)g2(a2019)= 
，对于g3(x),该函数在
上单调递减，在区间
上是常函数，
于是P3=g3(a1010)+g3(a1) =
，
对于g4(x),该函数在
和
递增,在
和
上递减,且是以
为周期的周期函数，故只需讨论
的情况，再2倍即可.仿前可知：
P4=2[g4(a505)g4(a1)+g4(a506)g4(a1010)]
<
，故P4<1，
综上可得： 
.
本题择A选项.
练习册系列答案
相关题目
【题目】设y=f(t)是某港口水的深度y(米)关于时间t(小时)的函数，其中
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系：
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 12 | 15.1 | 12.1 | 9.1 | 12 | 14.9 | 11.9 | 9 | 12.1 |
经长期观察，函数y=f(t)的图象可以近似地看成函数
的图象.⑴求
的解析式；⑵设水深不小于
米时，轮船才能进出港口。某轮船在一昼夜内要进港口靠岸办事，然后再出港。问该轮船最多能在港口停靠多长时间？
