题目内容
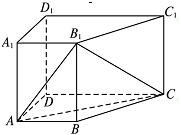
如图所示,在边长为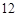 的正方形
的正方形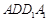 中,点
中,点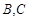 在线段
在线段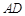 上,且
上,且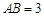 ,
,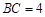 ,作
,作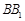 //
//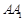 ,分别交
,分别交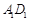 ,
,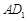 于点
于点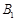 ,
,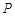 ,作
,作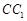 //
//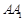 ,分别交
,分别交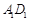 ,
,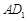 于点
于点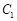 ,
,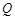 ,将该正方形沿
,将该正方形沿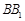 ,
,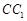 折叠,使得
折叠,使得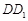 与
与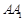 重合,构成如图所示的三棱柱
重合,构成如图所示的三棱柱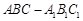 .
.
(1)求证: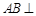 平面
平面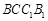 ;
;
(2)若点E为四边形BCQP内一动点,且二面角E-AP-Q的余弦值为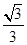 ,求|BE|的最小值.
,求|BE|的最小值.
(1)参考解析;(2)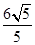
解析试题分析:(1)依题意可得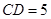 .即翻折后的
.即翻折后的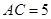 .所以由
.所以由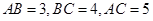 .可得
.可得 .又因为
.又因为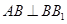 ,所以可得:
,所以可得: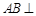 平面
平面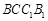 .
.
(2)依题意建立空间直角坐标系,由平面APQ写出其法向量.假设点E(m,n,0),根据平面APE写出其法向量.再由二面角E-AP-Q的余弦值为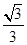 ,可得到关于m,n的方程m+2n-6=0.再由点B到直线的距离公式即可得到结论.
,可得到关于m,n的方程m+2n-6=0.再由点B到直线的距离公式即可得到结论.
(1)在正方形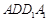 中,因为
中,因为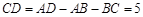 ,
,
所以三棱柱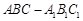 的底面三角形
的底面三角形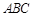 的边
的边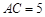 .
.
因为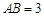 ,
,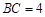 ,所以
,所以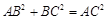 ,所以
,所以 .
.
因为四边形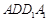 为正方形,
为正方形,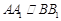 ,所以
,所以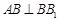 ,而
,而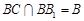 ,
,
所以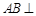 平面
平面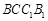 .----------- 4分
.----------- 4分
(2)因为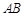 ,
, ,
,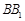 两两互相垂直.以
两两互相垂直.以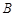 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系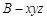 ,
,
则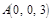 ,
, ,
,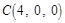 ,
, ,
,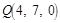 ,
,
所以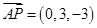 ,
,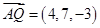 ,
,
设平面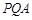 的一个法向量为
的一个法向量为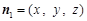 .
.
则由 ,即
,即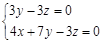 令
令 ,
,
则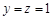 .所以
.所以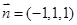 .
.
设点E(m,n,0),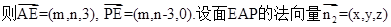

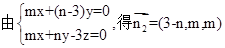 .由
.由 得:m+2n-6=0
得:m+2n-6=0
所以|BE|的最小值为点B到线段: m+2n-6="0" 的距离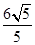 ------- 13分
------- 13分
考点:1.直线与平面的位置关系.2.二面角.3.空间直角坐标系的建立.4.点到直线的距离.

练习册系列答案
相关题目
 两两垂直,则
两两垂直,则

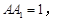
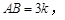
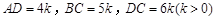 .
.
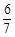 ,求k的值.
,求k的值. 和
和 所在平面互相垂直,且
所在平面互相垂直,且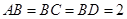 ,
, ,E、F分别为AC、DC的中点.
,E、F分别为AC、DC的中点.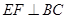 ;
;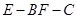 的正弦值.
的正弦值.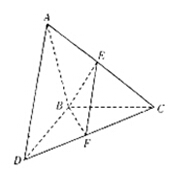
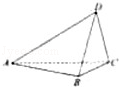
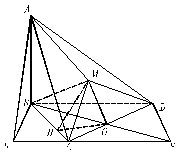
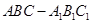 中,平面
中,平面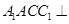 平面ABC,
平面ABC,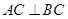 ,
,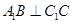 ,
,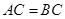 .
.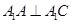 ;
;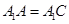 ,求二面角
,求二面角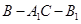 的余弦值.
的余弦值.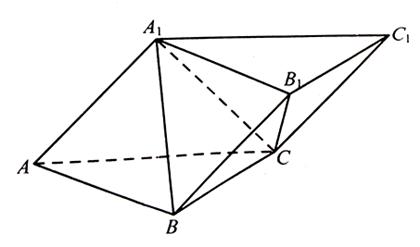
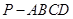 中,底面
中,底面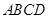 为矩形,侧棱
为矩形,侧棱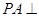 底面
底面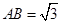 ,
,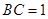 ,
,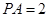 ,
, 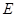 为
为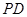 的中点.
的中点.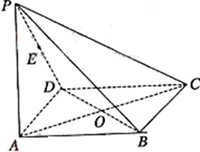
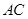 与
与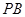 所成角的余弦值;
所成角的余弦值;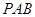 内找一点
内找一点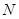 ,使
,使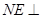 面
面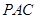 ,并求出点
,并求出点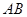 和
和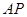 的距离.
的距离.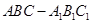 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是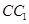 棱的中点,AE交
棱的中点,AE交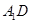 于点H.
于点H.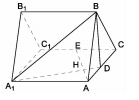
 平面
平面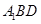 ;
;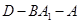 的余弦值;
的余弦值; 到平面
到平面