题目内容
已知函数f(x)=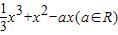 .
.(1)若a=8,求f(x)在区间[-6,3]上的最大值;
(2)若g(x)=
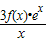 在(-∞,0)上恰有两个极值点,求a的取值范围.
在(-∞,0)上恰有两个极值点,求a的取值范围.
【答案】分析:(1)将a=8代入求出函数的解析式及导函数的解析式,分析函数的单调性,进而求出f(x)在区间[-6,3]上的最大值;
(2)若g(x)=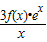 在(-∞,0)上恰有两个极值点,则g′(x)在(-∞,0)上恰有两个相异实根,根据韦达定理及△的符号构造不等式组可得答案.
在(-∞,0)上恰有两个极值点,则g′(x)在(-∞,0)上恰有两个相异实根,根据韦达定理及△的符号构造不等式组可得答案.
解答:解:(1)当a=8时,函数f(x)=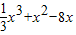 .
.
∴f′(x)=x2+2x-8
令f′(x)=0,则x=-4,或x=2
当-6<x<-4时,f′(x)>0,当2<x<3时,f′(x)>0,当-4<x<2时,f′(x)<0,
∴f(x)极大值=f(-4)=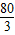
又∵f(-6)=12,f(3)=-6
f(x)的最大值为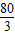
(2)∵g(x)=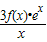 =(x2+3x-3a)ex
=(x2+3x-3a)ex
∴g′(x)=(x2+5x+3-3a)ex
∵g(x)=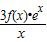 在(-∞,0)上恰有两个极值点,
在(-∞,0)上恰有两个极值点,
∴g(x)=0在(-∞,0)上恰有两个相异实根
即x2+5x+3-3a=0在(-∞,0)上恰有两个相异实根
∴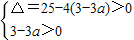
解得: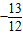 <a<1
<a<1
点评:本题考查的知识点是根据导数求闭区间上的最值,函数在某点取极值的条件,其中熟练掌握导数法在求函数单调性,最值,极值时的步骤是解答的关键.
(2)若g(x)=
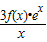 在(-∞,0)上恰有两个极值点,则g′(x)在(-∞,0)上恰有两个相异实根,根据韦达定理及△的符号构造不等式组可得答案.
在(-∞,0)上恰有两个极值点,则g′(x)在(-∞,0)上恰有两个相异实根,根据韦达定理及△的符号构造不等式组可得答案.解答:解:(1)当a=8时,函数f(x)=
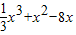 .
.∴f′(x)=x2+2x-8
令f′(x)=0,则x=-4,或x=2
当-6<x<-4时,f′(x)>0,当2<x<3时,f′(x)>0,当-4<x<2时,f′(x)<0,
∴f(x)极大值=f(-4)=
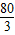
又∵f(-6)=12,f(3)=-6
f(x)的最大值为
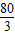
(2)∵g(x)=
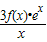 =(x2+3x-3a)ex
=(x2+3x-3a)ex∴g′(x)=(x2+5x+3-3a)ex
∵g(x)=
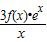 在(-∞,0)上恰有两个极值点,
在(-∞,0)上恰有两个极值点,∴g(x)=0在(-∞,0)上恰有两个相异实根
即x2+5x+3-3a=0在(-∞,0)上恰有两个相异实根
∴
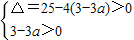
解得:
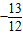 <a<1
<a<1点评:本题考查的知识点是根据导数求闭区间上的最值,函数在某点取极值的条件,其中熟练掌握导数法在求函数单调性,最值,极值时的步骤是解答的关键.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|