Question

已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0），则称以原点为圆心，r=

a2-b2

的圆为椭圆C的“知己圆”．
（Ⅰ）若椭圆过点（0，1），离心率e=

6

3

；求椭圆C方程及其“知己圆”的方程；
（Ⅱ）在（Ⅰ）的前提下，若过点（0，m）且斜率为1的直线截其“知己圆”的弦长为2，求m的值；
（Ⅲ）讨论椭圆C及其“知己圆”的位置关系．

Answer 1

分析：（I）根据椭圆过点（0，1），算出b=1．再由离心率e=

6

3

结合a²=b²+c²联解得到a²=3，c²=2，即可得到椭圆C的方程，最后根据椭圆的“知己圆”定义可得椭圆C的“知己圆”的方程．
（II）由椭圆C的“知己圆”的方程，得到其半径r=

2

，根据垂径定理算出弦长为2的弦心距d=1，因此设出线方程为y=x+m，利用点到直线的距离公式列式得到关于m的方程，解之即可得到实数m的值；
（III）根据椭圆C的“知己圆”定义，可得其方程为x²+y²=c²．由椭圆的形状，根据离心率e的范围加以讨论，即可得到椭圆C与它的“知己圆”的位置关系的三种不同情况，得到本题答案．

解答：解：（Ⅰ）∵椭圆C过点（0，1），∴

02

a2

+

12

b2

=1，可得b=1，
又∵椭圆C的离心率e=

6

3

，即

c

a

=

6

3

，且a²-c²=b²=1    …（2分）
解之得a²=3，c²=2
∴所求椭圆C的方程为：

x2

3

+y2=1                     …（4分）
由此可得“知己圆”的半径r=

a2-b2

=

2

∴椭圆C的“知己圆”的方程为：x²+y²=2        …（6分）
（Ⅱ）设过点（0，m）、且斜率为1的直线方程为y=x+m，即为x-y+m=0
∵直线截其“知己圆”的弦长l=2，
∴圆心到直线的距离为d=

r2-( 1 2 l)2

=

2-1

=1       …（8分）
由点到直线的距离公式，得d=

|0-0+m|

2

=1，解之得m=±

2

       …（10分）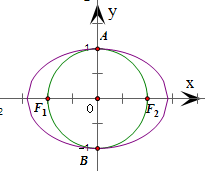
（Ⅲ）∵椭圆C的“知己圆”是以原点为圆心，r=

a2-b2

的圆
∴椭圆C的“知己圆”方程为x²+y²=c²
因此，①当c＜b时，即椭圆C的离心率e∈（0，

2

2

）时，椭圆C的“知己圆”与椭圆C没有公共点，由此可得“知己圆”在椭圆C内；…（12分）
当c=b时，即椭圆的离心率e=

2

2

时，椭圆C的“知己圆”与椭圆C有两个
公共点，由此可得“知己圆”与椭圆C相切于点（0，1）和（0，-1）；
当c＞b时，即椭圆C的离心率e∈（0，

2

2

）时，椭圆C的“知己圆”与椭圆C有四个公共点，由此可得“知己圆”与椭圆C是相交的位置关系． …（14分）

点评：本题给出椭圆的“知己圆”，求“知己圆”的方程并讨论椭圆与“知己圆”的位置关系，着重考查了椭圆的标准方程与简单几何性质、直线与圆的位置等知识，考查了分类讨论数学思想的应用，属于中档题．