题目内容
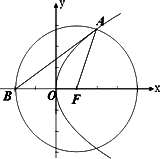
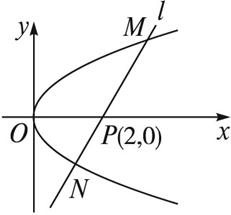
如图,点O为坐标原点,直线l经过抛物线C:y2=4x的焦点F.(Ⅰ)若点O到直线l的距离为
 ,求直线l的方程;
,求直线l的方程;(Ⅱ)设点A是直线l与抛物线C在第一象限的交点.点B是以点F为圆心,|FA|为半径的圆与x轴负半轴的交点.试判断直线AB与抛物线C的位置关系,并给出证明.

【答案】分析:法一:(Ⅰ)抛物线的焦点F(1,0),当直线l的斜率不存在时,即x=1不符合题意.当直线l的斜率存在时,设直线l的方程为:y=k(x-1),所以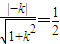 ,由此能求出直线l的方程.
,由此能求出直线l的方程.
(Ⅱ)直线AB与抛物线相切.设A(x,y),则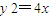 .因为|BF|=|AF|=x+1,所以B(-x,0),由此能够证明直线AB与抛物线相切.
.因为|BF|=|AF|=x+1,所以B(-x,0),由此能够证明直线AB与抛物线相切.
法二:(Ⅰ)同解法一.
(Ⅱ)直线AB与抛物线相切,设A(x,y),则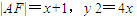 .设圆的方程为:
.设圆的方程为: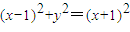 由此能够证明直线AB与抛物线相切.
由此能够证明直线AB与抛物线相切.
解答:解法一:(Ⅰ)抛物线的焦点F(1,0),…(1分)
当直线l的斜率不存在时,即x=1不符合题意.…(2分)
当直线l的斜率存在时,
设直线l的方程为:y=k(x-1),即kx-y-k=0.…(3分)
所以,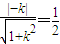 ,解得:
,解得: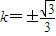 .…(5分)
.…(5分)
故直线l的方程为: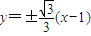 ,即
,即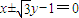 .…(6分)
.…(6分)
(Ⅱ)直线AB与抛物线相切,证明如下:…(7分)
(法一):设A(x,y),则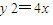 .…(8分)
.…(8分)
因为|BF|=|AF|=x+1,所以B(-x,0).…(9分)
所以直线AB的方程为: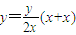 ,
,
整理得: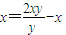 …(1)
…(1)
把方程(1)代入y2=4x得: ,…(10分)
,…(10分)
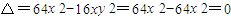 ,
,
所以直线AB与抛物线相切.…(12分)
解法二:(Ⅰ)同解法一.
(Ⅱ)直线AB与抛物线相切,证明如下:…(7分)
设A(x,y),则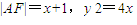 .…(8分)
.…(8分)
设圆的方程为: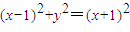 ,…(9分)
,…(9分)
当y=0时,得x=1±(x+1),
因为点B在x轴负半轴,所以B(-x,0).…(9分)
所以直线AB的方程为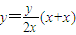 ,
,
整理得: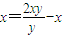 …(1)
…(1)
把方程(1)代入y2=4x得: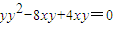 ,…(10分)
,…(10分)
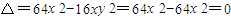 ,
,
所以直线AB与抛物线相切.…(12分)
点评:本小题考查抛物线的标准方程、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想等.
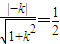 ,由此能求出直线l的方程.
,由此能求出直线l的方程.(Ⅱ)直线AB与抛物线相切.设A(x,y),则
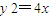 .因为|BF|=|AF|=x+1,所以B(-x,0),由此能够证明直线AB与抛物线相切.
.因为|BF|=|AF|=x+1,所以B(-x,0),由此能够证明直线AB与抛物线相切.法二:(Ⅰ)同解法一.
(Ⅱ)直线AB与抛物线相切,设A(x,y),则
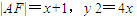 .设圆的方程为:
.设圆的方程为: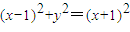 由此能够证明直线AB与抛物线相切.
由此能够证明直线AB与抛物线相切.解答:解法一:(Ⅰ)抛物线的焦点F(1,0),…(1分)
当直线l的斜率不存在时,即x=1不符合题意.…(2分)
当直线l的斜率存在时,
设直线l的方程为:y=k(x-1),即kx-y-k=0.…(3分)
所以,
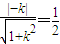 ,解得:
,解得: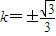 .…(5分)
.…(5分)故直线l的方程为:
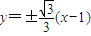 ,即
,即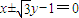 .…(6分)
.…(6分)(Ⅱ)直线AB与抛物线相切,证明如下:…(7分)
(法一):设A(x,y),则
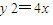 .…(8分)
.…(8分)因为|BF|=|AF|=x+1,所以B(-x,0).…(9分)
所以直线AB的方程为:
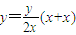 ,
,整理得:
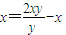 …(1)
…(1)把方程(1)代入y2=4x得:
 ,…(10分)
,…(10分)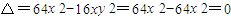 ,
,所以直线AB与抛物线相切.…(12分)
解法二:(Ⅰ)同解法一.
(Ⅱ)直线AB与抛物线相切,证明如下:…(7分)
设A(x,y),则
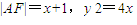 .…(8分)
.…(8分)设圆的方程为:
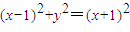 ,…(9分)
,…(9分)当y=0时,得x=1±(x+1),
因为点B在x轴负半轴,所以B(-x,0).…(9分)
所以直线AB的方程为
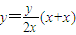 ,
,整理得:
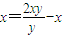 …(1)
…(1)把方程(1)代入y2=4x得:
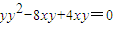 ,…(10分)
,…(10分)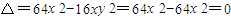 ,
,所以直线AB与抛物线相切.…(12分)
点评:本小题考查抛物线的标准方程、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
如图已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).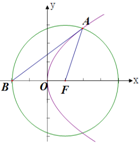 (2012•泉州模拟)如图,点O为坐标原点,直线l经过抛物线C:y2=4x的焦点F.
(2012•泉州模拟)如图,点O为坐标原点,直线l经过抛物线C:y2=4x的焦点F.