题目内容
下列命题中，真命题是（ ）A．?x∈R，e
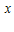≤0B．?x∈R，2x＞x2
C．a=b=0的充要条件是
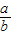=-1D．若x，y∈R，且x+y＞2，则x，y至少有一个大于1
【答案】分析：利用全称命题和特称命题的定义判断A，B．利用充要条件和必要条件的定义判断C．利用反证法证明D．
解答：解：A，根据指数函数的性质可知ex＞0恒成立，所以A错误．
B．当x=-1时，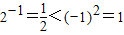
，所以B错误．
C．若a=b=0时，满足a+b=0，但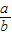
=-1，不成立，所以C错误．
D．假设x，y都小于1，则x＜1，y＜1，所以x+y＜2与x+y＞2矛盾，所以假设不成立，所以D正确．
点评：本题主要考查命题的真假判断，比较基础．
解答：解：A，根据指数函数的性质可知ex＞0恒成立，所以A错误．
B．当x=-1时，
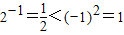，所以B错误．C．若a=b=0时，满足a+b=0，但
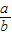=-1，不成立，所以C错误．D．假设x，y都小于1，则x＜1，y＜1，所以x+y＜2与x+y＞2矛盾，所以假设不成立，所以D正确．
点评：本题主要考查命题的真假判断，比较基础．
练习册系列答案
相关题目
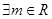，使函数
是偶函数
，使函数
≤0
=-1