题目内容
已知∠A为△ABC的内角，若
=
- A.
- B.
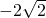
- C.
- D.-2
B
分析：将已知等式左边中的角提取-1后，根据正弦函数为奇函数化简，再利用诱导公式变形后，求出cosA的值，由A为三角形的内角，利用同角三角函数间的基本关系求出sinA的值，最后再利用同角三角函数间的基本关系弦化切，即可求出tanA的值．
解答：∵sin（A-
）=sin[-（-A）]=-sin（-A）=-cosA=
，
∴cosA=-，又∠A为△ABC的内角，
∴sinA=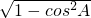
=
，
则tanA=
=-2
．
故选B
点评：此题考查了诱导公式，正弦函数的奇偶性，以及同角三角函数间的基本关系，熟练掌握同角三角函数间的基本关系是解本题的关键．
分析：将已知等式左边中的角提取-1后，根据正弦函数为奇函数化简，再利用诱导公式变形后，求出cosA的值，由A为三角形的内角，利用同角三角函数间的基本关系求出sinA的值，最后再利用同角三角函数间的基本关系弦化切，即可求出tanA的值．
解答：∵sin（A-
）=sin[-（-A）]=-sin（-A）=-cosA=，∴cosA=-
，又∠A为△ABC的内角，∴sinA=
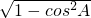=，则tanA=
=-2．故选B
点评：此题考查了诱导公式，正弦函数的奇偶性，以及同角三角函数间的基本关系，熟练掌握同角三角函数间的基本关系是解本题的关键．
练习册系列答案
相关题目
=（
）
B．
C．
D．-2