题目内容
已知函数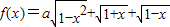 的最大值为g(a).
的最大值为g(a).(1)设
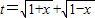 ,求t的取值范围;
,求t的取值范围;(2)求g(a).
【答案】分析:(1)利用函数的定义域及平方法求值域;
(2)利用换元法将函数变为关于t的函数,再用分类讨论思想,求一元二次函数在定区间上的最大值即可.
解答:解:(1)t=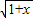 +
+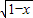 的定义域是[-1,1],
的定义域是[-1,1],
t2=2+2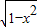 ∈[2,4],∵t>0,
∈[2,4],∵t>0,
∴t∈[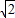 ,2]
,2]
∴t的取值范围是[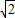 ,2].
,2].
(2)由(1)知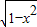 =
= t2-1,
t2-1,
∴f(t)= at2+t-a,t∈[
at2+t-a,t∈[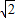 ,2]
,2]
①当a>0时,f(t)在[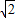 ,2]上递增,
,2]上递增,
∴g(a)=f(2)=2a+2-a=a+2;
②当a=0时,f(t)=t,在[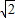 ,2]上递增,
,2]上递增,
∴g(a)=2;
③当a<0时,分三种情况讨论,
A:- <a<0,-
<a<0,-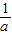 >2,∴g(a)=f(2)=a+2;
>2,∴g(a)=f(2)=a+2;
B:a<-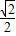 ,-
,-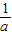 <
<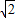 ,∴g(a)=f(
,∴g(a)=f(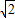 )=
)=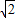 ;
;
C:-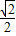 ≤a≤-
≤a≤- ,-
,-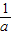 ∈[
∈[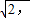 2],∴g(a)=-a-
2],∴g(a)=-a-
综上g(a)=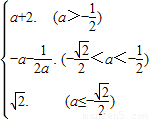
点评:本题考查函数的值域与最值.含有参数的函数在定区间上的最值问题常用分类讨论思想求解.
(2)利用换元法将函数变为关于t的函数,再用分类讨论思想,求一元二次函数在定区间上的最大值即可.
解答:解:(1)t=
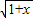 +
+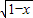 的定义域是[-1,1],
的定义域是[-1,1],t2=2+2
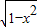 ∈[2,4],∵t>0,
∈[2,4],∵t>0,∴t∈[
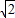 ,2]
,2]∴t的取值范围是[
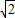 ,2].
,2].(2)由(1)知
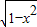 =
= t2-1,
t2-1,∴f(t)=
 at2+t-a,t∈[
at2+t-a,t∈[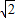 ,2]
,2]①当a>0时,f(t)在[
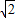 ,2]上递增,
,2]上递增,∴g(a)=f(2)=2a+2-a=a+2;
②当a=0时,f(t)=t,在[
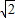 ,2]上递增,
,2]上递增,∴g(a)=2;
③当a<0时,分三种情况讨论,
A:-
 <a<0,-
<a<0,-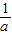 >2,∴g(a)=f(2)=a+2;
>2,∴g(a)=f(2)=a+2;B:a<-
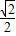 ,-
,-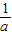 <
<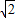 ,∴g(a)=f(
,∴g(a)=f(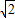 )=
)=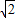 ;
;C:-
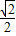 ≤a≤-
≤a≤- ,-
,-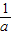 ∈[
∈[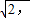 2],∴g(a)=-a-
2],∴g(a)=-a-
综上g(a)=
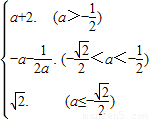
点评:本题考查函数的值域与最值.含有参数的函数在定区间上的最值问题常用分类讨论思想求解.

练习册系列答案
相关题目
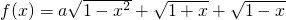 的最大值为g(a).
的最大值为g(a).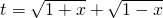 ,求t的取值范围;
,求t的取值范围;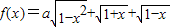 的最大值为g(a).
的最大值为g(a).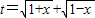 ,求t的取值范围;
,求t的取值范围; 的最大值为g(a).
的最大值为g(a).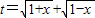 ,求t的取值范围;
,求t的取值范围; 的最大值为g(a).
的最大值为g(a).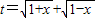 ,求t的取值范围;
,求t的取值范围;