题目内容
设数列{an}的前n项和为Sn,已知 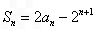 (n∈N*).
(n∈N*).
(1)求数列{an}的通项公式;
(2)设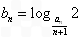 ,数列{bn}的前n项和为Bn,若存在整数m,使对任意n∈N*且n ≥2,都有
,数列{bn}的前n项和为Bn,若存在整数m,使对任意n∈N*且n ≥2,都有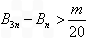 成立,求m的最大值;
成立,求m的最大值;
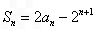 (n∈N*).
(n∈N*). (1)求数列{an}的通项公式;
(2)设
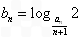 ,数列{bn}的前n项和为Bn,若存在整数m,使对任意n∈N*且n ≥2,都有
,数列{bn}的前n项和为Bn,若存在整数m,使对任意n∈N*且n ≥2,都有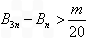 成立,求m的最大值;
成立,求m的最大值; 解:(1)由Sn=2an-2n+1,得Sn-1=2an-1-2n(n≥2).
两式相减,得an=2an-2an-1-2n,即an-2an-1=2n(n≥2).
于是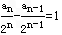 ,所以数列
,所以数列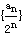 是公差为1 的等差数列.
是公差为1 的等差数列.
又S1=2a1-22 ,所以a1=4 .
所以 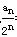 =2+(n-1)=n+1,
=2+(n-1)=n+1,
故an=(n+1)·2n.
(2)因为bn=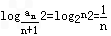 ,则
,则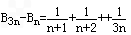
令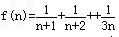 则
则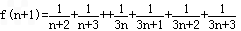
所以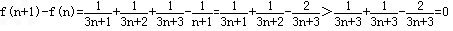 。
。
即f(n+1)>f(n),所以数列{f(n)}为递增数列.
所以当n≥2时,f(n)的最小值为f(2)=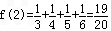
据题意,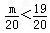 ,即m <19 .
,即m <19 .
又m 为整数, 故m 的最大值为18 .

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目