题目内容
已知公差不为零的等差数列{an}中,M=an•an+3,N=an+1•an+2,则M与N的大小关系是
M<N
M<N
.分析:设等差数列的公差为d,(d≠0),将M与N用an表示,作差即可.
解答:解:设{an}的公差为d,则d≠0,
∵M=an•an+3,N=an+1•an+2,
∴M-N=an(an+3d)-[(an+d)(an+2d)]
=an2+3dan-an2-3dan-2d2
=-2d2<0,
∴M<N.
故答案为:M<N.
∵M=an•an+3,N=an+1•an+2,
∴M-N=an(an+3d)-[(an+d)(an+2d)]
=an2+3dan-an2-3dan-2d2
=-2d2<0,
∴M<N.
故答案为:M<N.
点评:本题考查等差数列的通项公式,比较M与N的大小,作差是关键,属于基础题.

练习册系列答案
相关题目
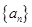 与公比为
与公比为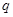 的等比数列
的等比数列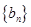 有相同的首项,同时满足
有相同的首项,同时满足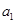 ,
,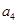 ,
,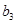 成等比,
成等比, ,
,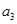 ,
,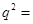 ( )
( )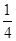 B.
B.
 C.
C.
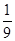 D.
D.