题目内容
已知f（x）的反函数f-1（x）=log2（x+2），则方程f（x-1）=0的根为（ ）
A．-
| B．0 | C．1 | D．2 |
∵f-1（x）=log2（x+2），
∴f（x）=2x-2
若f（x-1）=0
则2x-1-2=0
即x-1=1
解得x=2
故选D
∴f（x）=2x-2
若f（x-1）=0
则2x-1-2=0
即x-1=1
解得x=2
故选D
练习册系列答案
相关题目
已知f（x）的反函数为f-1(x)=(
)x，则f（4-x2）的单调递减区间是（ ）
| 1 |
| 2 |
| A、（-2，0） |
| B、（-∞，0） |
| C、（0，+∞） |
| D、（0，2） |
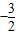
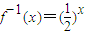，则f（4-x2）的单调递减区间是（ ）