题目内容
下列命题中:
(1)平行于同一直线的两个平面平行;
(2)平行于同一平面的两个平面平行;
(3)垂直于同一直线的两直线平行;
(4)垂直于同一平面的两直线平行.
其中正确的个数有
(1)平行于同一直线的两个平面平行;
(2)平行于同一平面的两个平面平行;
(3)垂直于同一直线的两直线平行;
(4)垂直于同一平面的两直线平行.
其中正确的个数有
2
2
.分析:(1)反例为:把一支笔放在打开的课本之间,一支笔平行于两平面的交线;
(2)利用平行平面的传递性即可判断出;
(3)反例:正方体的棱长所在的直线可能平行、相交或为异面直线;
(4)根据线面垂直的性质可得:垂直于同一平面的两直线平行.
(2)利用平行平面的传递性即可判断出;
(3)反例:正方体的棱长所在的直线可能平行、相交或为异面直线;
(4)根据线面垂直的性质可得:垂直于同一平面的两直线平行.
解答:解:(1)不正确,反例:把一支笔放在打开的课本之间,一支笔平行于两平面的交线;
(2)正确,此结论为平行平面的传递性;
(3)不正确,反例:正方体的棱长所在的直线可能平行、相交或为异面直线;
(4)根据线面垂直的性质可得:垂直于同一平面的两直线平行,因此正确.
综上可知:只有(2)(4)正确;
故答案为2.
(2)正确,此结论为平行平面的传递性;
(3)不正确,反例:正方体的棱长所在的直线可能平行、相交或为异面直线;
(4)根据线面垂直的性质可得:垂直于同一平面的两直线平行,因此正确.
综上可知:只有(2)(4)正确;
故答案为2.
点评:熟练空间中的线线、线面、面面的位置关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
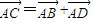 ,则ABCD为平行四边形
,则ABCD为平行四边形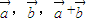 为非零向量,且a+b平分a与b的夹角,则|a|=|b|
为非零向量,且a+b平分a与b的夹角,则|a|=|b|