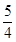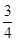题目内容
知函数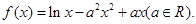
(1)若函数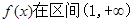 上是单调减函数,求实数a的取值范围;
上是单调减函数,求实数a的取值范围;
(2)讨论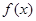 的极值;
的极值;
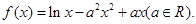
(1)若函数
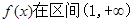 上是单调减函数,求实数a的取值范围;
上是单调减函数,求实数a的取值范围;(2)讨论
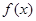 的极值;
的极值;(1)实数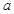 的以值范围是
的以值范围是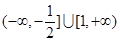
(2)①当 时,
时,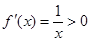 , ∴
, ∴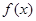 的增区间为
的增区间为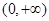 ,此时
,此时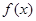 无极值
无极值
②当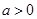 时,令
时,令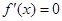 ,得
,得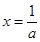 或
或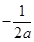 (舍去)
(舍去)
∴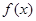 的增区间为
的增区间为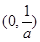 ,减区间为
,减区间为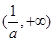
所以此时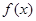 有极大值为
有极大值为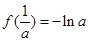 ,无极小值.
,无极小值.
③当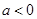 时,令
时,令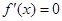 ,得
,得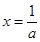 (舍去)或
(舍去)或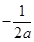
∴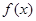 的增区间为
的增区间为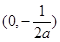 ,减区间为
,减区间为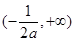 .
.
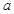 的以值范围是
的以值范围是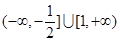
(2)①当
 时,
时,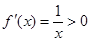 , ∴
, ∴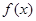 的增区间为
的增区间为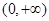 ,此时
,此时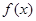 无极值
无极值②当
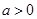 时,令
时,令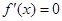 ,得
,得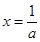 或
或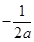 (舍去)
(舍去)∴
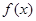 的增区间为
的增区间为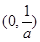 ,减区间为
,减区间为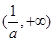
所以此时
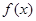 有极大值为
有极大值为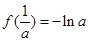 ,无极小值.
,无极小值.③当
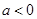 时,令
时,令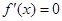 ,得
,得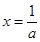 (舍去)或
(舍去)或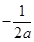
∴
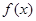 的增区间为
的增区间为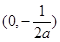 ,减区间为
,减区间为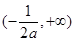 .
.本试题主要是考查了导数在研究函数中的运用
(1)因为①当 时,
时,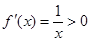 , ∴
, ∴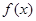 在区间
在区间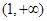 上为增函数,不合题意.
上为增函数,不合题意.
②当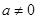 时,要使函数
时,要使函数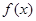 在区间
在区间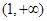 上是减函数.
上是减函数.
只需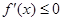 在区间
在区间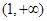 上恒成立,解得。
上恒成立,解得。
(2) 函数 的定义域为
的定义域为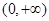
∴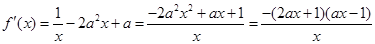 ,对与参数a分类讨论得到单调性
,对与参数a分类讨论得到单调性
(1)因为①当
 时,
时,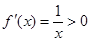 , ∴
, ∴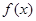 在区间
在区间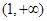 上为增函数,不合题意.
上为增函数,不合题意.②当
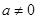 时,要使函数
时,要使函数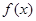 在区间
在区间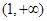 上是减函数.
上是减函数.只需
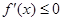 在区间
在区间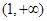 上恒成立,解得。
上恒成立,解得。(2) 函数
 的定义域为
的定义域为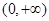
∴
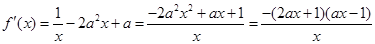 ,对与参数a分类讨论得到单调性
,对与参数a分类讨论得到单调性
练习册系列答案
相关题目
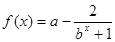
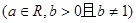
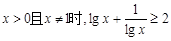
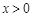 ,
,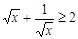
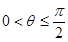 ,
,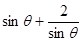 的最小值为
的最小值为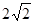
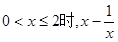 无最大值
无最大值 上的函数
上的函数 满足:①
满足:① 是奇函数;②当
是奇函数;②当 时,函数
时,函数 ,则
,则 的值( )
的值( ) 有负根,则a的取值范围是_______________
有负根,则a的取值范围是_______________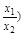 +f(x2)=f(x1),且当x>1时,f(x)<0.
+f(x2)=f(x1),且当x>1时,f(x)<0.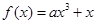 恰有3个单调区间,则a的取值范围为
恰有3个单调区间,则a的取值范围为  的最大值是( )
的最大值是( )