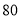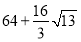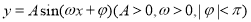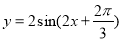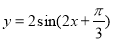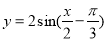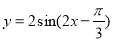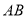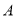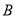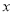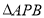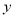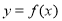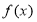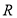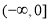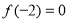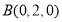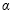题目内容
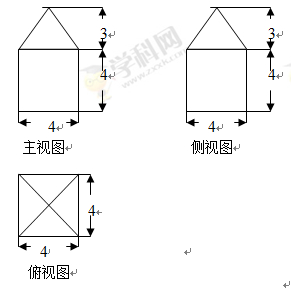
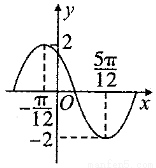
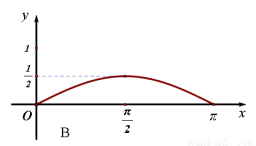
已知函数
的部分图像如图所示.
（1）求
的值；
（2）求函数
的单调递增区间.
（1）
；（2）
的单调递增区间是
.
【解析】
试题分析：（1）从图中观察到该函数的最小正周期
，从而由公式
得到
的值；再由
得到
的值，进而用
得到
的值；（2）由
的表达式确定
，将
当成整体，由正弦函数的单调递增区间可求得该函数的单调递增区间.
试题解析：（1）由题设图像知，周期
2分
，由
，得
4分
5分
所以 6分
（2）由（1）得
7分
10分
由
，得
的单调递增区间是 12分.
考点：三角函数的图像与性质.
练习册系列答案
阅读快车系列答案
相关题目
