题目内容
双曲线x2-y2=1右支上点P(a,b)到其第一、三象限渐近线距离为 ,则a+b=
,则a+b=
- A.

- B.

- C.

- D.±2
B
分析:P(a,b)点在双曲线上,则有a2-b2=1,即(a+b)(a-b)=1.根据点到直线的距离公式能够求出a-b的值,由此能够得到a+b的值.
解答:P(a,b)点在双曲线上,则有a2-b2=1,即(a+b)(a-b)=1.
d=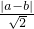 =
= ,
,
∴|a-b|=2.
又P点在右支上,则有a>b,
∴a-b=2.
∴|a+b|×2=1,a+b=- ,
,
故选B.
点评:本小题主要考查双曲线的简单性质、不等式表示的区域、点到直线的距离等基础知识,考查运算求解能力,考查数形结合思想,属于基础题.
分析:P(a,b)点在双曲线上,则有a2-b2=1,即(a+b)(a-b)=1.根据点到直线的距离公式能够求出a-b的值,由此能够得到a+b的值.
解答:P(a,b)点在双曲线上,则有a2-b2=1,即(a+b)(a-b)=1.
d=
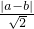 =
= ,
,∴|a-b|=2.
又P点在右支上,则有a>b,
∴a-b=2.
∴|a+b|×2=1,a+b=-
 ,
,故选B.
点评:本小题主要考查双曲线的简单性质、不等式表示的区域、点到直线的距离等基础知识,考查运算求解能力,考查数形结合思想,属于基础题.

练习册系列答案
相关题目
若椭圆
+
=1过抛物线y2=8x的焦点,且与双曲线x2-y2=1有相同的焦点,则该椭圆的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2+
|