题目内容
已知数列 满足:
满足: ,其中
,其中 .
.(1)当
 时,求{an}的通项公式;
时,求{an}的通项公式;(2)在(1)的条件下,若数列{bn}中,
 ,且b1=1.求证:对于
,且b1=1.求证:对于 恒成立;
恒成立;(3)对于
 ,设{an}的前n项和为Sn,试比较Sn+2与
,设{an}的前n项和为Sn,试比较Sn+2与 的大小.
的大小.
【答案】分析:(1)先确定数列{an}是首项为a1=1,公比为 的等比数列,再求数列{an}的通项公式;
的等比数列,再求数列{an}的通项公式;
(2)由(1)得,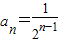 ,从而可得
,从而可得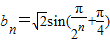 确定角的范围,即可得到结论;
确定角的范围,即可得到结论;
(3)解法一:先确定{an}的通项公式,再分组求和,作差比较可得结论;
解法二:先确定{an}的通项公式,再分组求和,利用放缩法可得结论;
解答:(1)解:当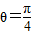 时,
时,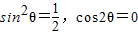 ,∴
,∴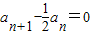 ,即
,即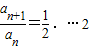 分
分
故数列{an}是首项为a1=1,公比为 的等比数列.
的等比数列.
故数列{an}的通项公式为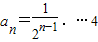 分
分
(2)证明:由(1)得,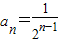 ,
,
∴当n∈N*,n≥2时,有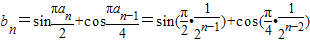 =
=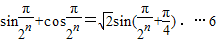 分
分
b1=1也满足上式,故当n∈N*时,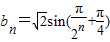 .
.
∵n∈N*,
∴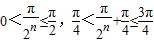 ,
,
∴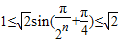 ,即
,即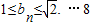 分
分
(3)解:解法一:由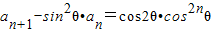 得:
得: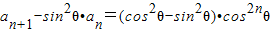 ,
,
∴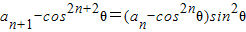 ,即
,即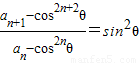 ,
,
∴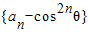 是首项为
是首项为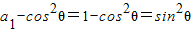 ,公比为sin2θ的等比数列,
,公比为sin2θ的等比数列,
故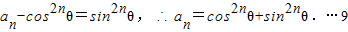 分
分
∴Sn=a1+a2+…+an=(cos2θ+cos4θ+…+cos2nθ)+(sin2θ+sin4θ+…+sin2nθ)
=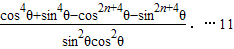 分
分
因此,Sn+2-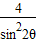 =
=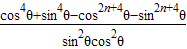 +2-
+2-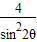
=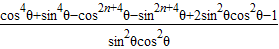
=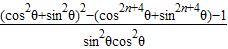
=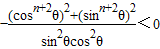 ,
,
∴Sn+2<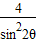 .…(14分)
.…(14分)
解法二:同解法一得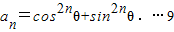 分
分
∵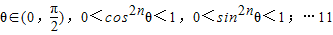 分
分
∴Sn=a1+a2+…+an=(cos2θ+cos4θ+…+cos2nθ)+(sin2θ+sin4θ+…+sin2nθ)=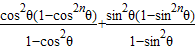
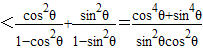 =
=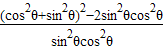 =
=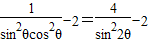
∴Sn+2<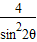 .…(14分)
.…(14分)
(其他解法酌情给分)
点评:本题考查数列的通项,考查不等式的证明,考查大小比较,确定数列通项,掌握求和方法是关键.
 的等比数列,再求数列{an}的通项公式;
的等比数列,再求数列{an}的通项公式;(2)由(1)得,
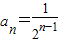 ,从而可得
,从而可得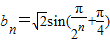 确定角的范围,即可得到结论;
确定角的范围,即可得到结论;(3)解法一:先确定{an}的通项公式,再分组求和,作差比较可得结论;
解法二:先确定{an}的通项公式,再分组求和,利用放缩法可得结论;
解答:(1)解:当
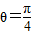 时,
时,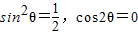 ,∴
,∴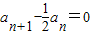 ,即
,即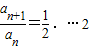 分
分故数列{an}是首项为a1=1,公比为
 的等比数列.
的等比数列.故数列{an}的通项公式为
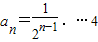 分
分(2)证明:由(1)得,
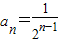 ,
,∴当n∈N*,n≥2时,有
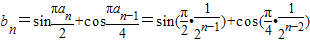 =
=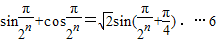 分
分b1=1也满足上式,故当n∈N*时,
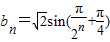 .
.∵n∈N*,
∴
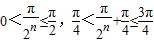 ,
,∴
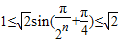 ,即
,即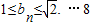 分
分(3)解:解法一:由
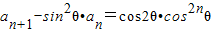 得:
得: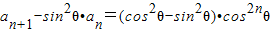 ,
,∴
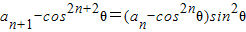 ,即
,即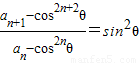 ,
,∴
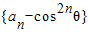 是首项为
是首项为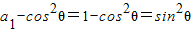 ,公比为sin2θ的等比数列,
,公比为sin2θ的等比数列,故
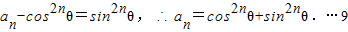 分
分∴Sn=a1+a2+…+an=(cos2θ+cos4θ+…+cos2nθ)+(sin2θ+sin4θ+…+sin2nθ)
=
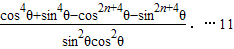 分
分因此,Sn+2-
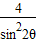 =
=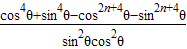 +2-
+2-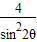
=
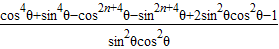
=
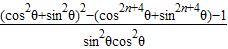
=
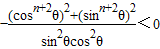 ,
,∴Sn+2<
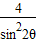 .…(14分)
.…(14分)解法二:同解法一得
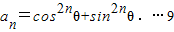 分
分∵
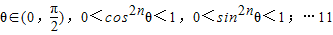 分
分∴Sn=a1+a2+…+an=(cos2θ+cos4θ+…+cos2nθ)+(sin2θ+sin4θ+…+sin2nθ)=
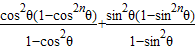
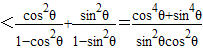 =
=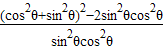 =
=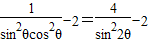
∴Sn+2<
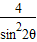 .…(14分)
.…(14分)(其他解法酌情给分)
点评:本题考查数列的通项,考查不等式的证明,考查大小比较,确定数列通项,掌握求和方法是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
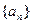 满足:
满足: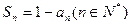 ,其中
,其中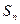 为数列
为数列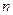 项和.
项和.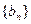 满足:
满足: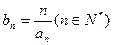 ,试求
,试求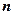 项和公式
项和公式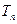 .
.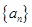 满足:
满足: (其中常数
(其中常数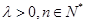 ).
).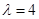 时,数列
时,数列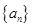 满足:
满足: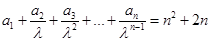 (其中常数
(其中常数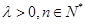 ).
).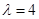 时,数列
时,数列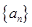 满足:
满足: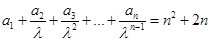 (其中常数
(其中常数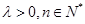 ).
).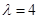 时,数列
时,数列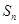 为数列
为数列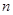 项和.求证:若任意
项和.求证:若任意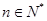 ,
,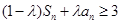
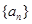 满足:
满足: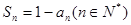 ,其中
,其中 为
为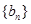 满足
满足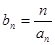 ,求
,求