题目内容
(本题满分12分)如图所示,正方形 与直角梯形
与直角梯形 所在平面互相垂直,
所在平面互相垂直, ,
, ,
, .
.

(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)求四面体 的体积.
的体积.
(1)见解析;(2)见解析;(3)
【解析】
试题分析:(1)由 ,
, 易得
易得 平面
平面 ;(2)易在平面
;(2)易在平面 内找一
内找一 中线与
中线与 平行从而得到
平行从而得到 平面
平面 ;(3)亦求
;(3)亦求 的体积关键在于找准底面及其高,本题易得
的体积关键在于找准底面及其高,本题易得 为底面且其高为
为底面且其高为 .
.
试题解析:(1)证明:因为平面
 平面
平面 ,
, ,
,
所以 平面
平面 ,所以
,所以 .
.
因为 是正方形,所以
是正方形,所以 ,
,
所以 平面
平面 .
.
(2)设 ,取
,取 中点
中点 ,连结
,连结 ,
,
所以,

 .
.
因为 ,
, ,
,
所以

 ,
,
从而四边形 是平行四边形,
是平行四边形, .
.
因为 平面
平面 ,
, 平面
平面 ,
,
所以 平面
平面 ,即
,即 平面
平面 .
.
(3)四面体 的体积
的体积
 .
.
考点:线面垂直关系证明、线面平行关系证明、几何体的体积
考点分析: 考点1:点、线、面之间的位置关系 考点2:柱、锥、台、球的表面积和体积 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,
, 是
是 的中点,
的中点, 是
是 与
与 的交点.
的交点.
 平面
平面 ;
; 平面
平面 .
. 的内角
的内角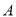 ,
, ,
, 所对的边长分别为
所对的边长分别为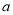 ,
,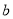 ,
,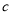 且
且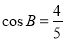 ,
, .
. ,求
,求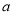 的值;
的值;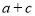 的值
的值 中,若
中,若 ,则
,则 的值为 ( )
的值为 ( ) 中,
中, ,
, ,三角形面积
,三角形面积 ,则
,则 等于 ( )
等于 ( ) B.
B. C.
C. 或
或 D.
D. 或
或
 .
. 上的点到直线
上的点到直线 的距离最大值是( )
的距离最大值是( )  C.
C. D.
D.
 ,设
,设 ,
,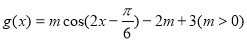 ,若对任意
,若对任意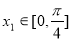 都存在
都存在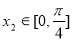 ,使得
,使得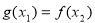 成立。则实数
成立。则实数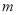 的取值范围是
的取值范围是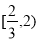 B.
B.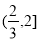 C.
C.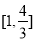 D.
D.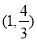
 ,M是
,M是 上的动点,则|MN|的最小值是 。
上的动点,则|MN|的最小值是 。