题目内容
如图,已知多面体ABCDE中,AB⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1,F是CD的中点.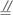
(1)求证:AF∥平面BCE;
(2)求多面体ABCDE的体积;
(3)求二面角C-BE-D的正切值.
(1)证明:如图,取CE中点M,连结FM、BM,则有FM![]() DE
DE![]() AB,
AB,

∴四边形AFMB是平行四边形.
∴AF∥BM.
∵BM![]() 平面BCE,AF
平面BCE,AF![]() 平面BCE,
平面BCE,
∴AF∥平面BCE.
(2)解:由DE⊥平面ACD,则DE⊥AF,
又△ACD是等边三角形,则AF⊥CD.而CD∩DE=D,因此AF⊥面CDE.又BM∥AF,则BM⊥平面CDE.VABCDE=VB—ACD+VB—CDE=![]() .
.
(3)解:设G为AD中点,连结CG、BG、EG,则CG⊥AD.
由DE⊥平面ACD,CG![]() 平面ACD,则DE⊥CG,
平面ACD,则DE⊥CG,
又AD∩DE=D,∴CG⊥平面ADEB.
作GH⊥BE于H,连结CH,则CH⊥BE,
∴∠CHG为二面角CBED的平面角,
由已知AB=1,DE=AD=2,则CG=![]() .
.
∴S△GBE=![]() (1+2)·2-
(1+2)·2-![]() ×1×1-
×1×1-![]() ×2×1=
×2×1=![]() .易知BE=
.易知BE=![]() ,∴S△GBE=
,∴S△GBE=![]() .
.
∴GH=![]() .∴tan∠CHG=
.∴tan∠CHG=![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
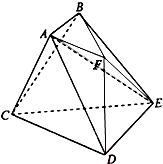 如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且
如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且 如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点.
如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.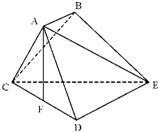 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.