题目内容
正方体ABCD-A1B1C1D1中,EF⊥AC,EF⊥A1D则EF和BD1的关系是________.
平行
分析:法一:先证EF垂直面AB1C,然后再BD1证垂直面AB1C,最后利用直线与平面垂直的性质定理即可得知结论;
法二:建立以D1为原点的空间直角坐标系D1-xyz,设正方形的边长为1,利用向量法,我们易求出BD1与A1D和AC都垂直,根据共垂线的性质,可以得到答案.
解答: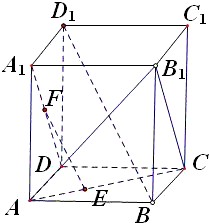 解:法一:根据图象可知:
解:法一:根据图象可知:
EF⊥AC,EF⊥A1D,A1D∥B1C,B1C⊥EF,AC∩B1C=C,
∴EF⊥面AB1C,而BD1⊥面AB1C,即BD1∥EF.
法二:建立以D1为原点的空间直角坐标系D1-xyz,且设正方形的边长为1
所以就有D1(0,0,0),B(1,1,0),A1(1,0,0),D(0,0,1),A(1,0,1),C(0,1,1)
所以 =(-1,0,1),
=(-1,0,1), =(-1,1,0),
=(-1,1,0),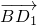 =(-1,-1,1)
=(-1,-1,1)
所以 •
•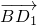 =-1+1=0 所以A1D⊥BD1,
=-1+1=0 所以A1D⊥BD1,
 •
•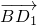 =1-1=0 所以AC⊥BD1,
=1-1=0 所以AC⊥BD1,
所以BD1与A1D和AC都垂直
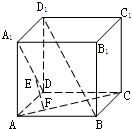 又∵EF是AC、A1D的公共垂线,
又∵EF是AC、A1D的公共垂线,
∴BD1∥EF.
故答案为:平行.
点评:本题主要考查直线与平面垂直的性质定理的应用,空间中直线与直线之间的位置关系,其中建立空间坐标系,借助向量分析直线与直线之间的位置关系是解答本题的关键.
分析:法一:先证EF垂直面AB1C,然后再BD1证垂直面AB1C,最后利用直线与平面垂直的性质定理即可得知结论;
法二:建立以D1为原点的空间直角坐标系D1-xyz,设正方形的边长为1,利用向量法,我们易求出BD1与A1D和AC都垂直,根据共垂线的性质,可以得到答案.
解答:
 解:法一:根据图象可知:
解:法一:根据图象可知:EF⊥AC,EF⊥A1D,A1D∥B1C,B1C⊥EF,AC∩B1C=C,
∴EF⊥面AB1C,而BD1⊥面AB1C,即BD1∥EF.
法二:建立以D1为原点的空间直角坐标系D1-xyz,且设正方形的边长为1
所以就有D1(0,0,0),B(1,1,0),A1(1,0,0),D(0,0,1),A(1,0,1),C(0,1,1)
所以
 =(-1,0,1),
=(-1,0,1), =(-1,1,0),
=(-1,1,0),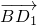 =(-1,-1,1)
=(-1,-1,1)所以
 •
•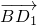 =-1+1=0 所以A1D⊥BD1,
=-1+1=0 所以A1D⊥BD1, •
•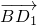 =1-1=0 所以AC⊥BD1,
=1-1=0 所以AC⊥BD1,所以BD1与A1D和AC都垂直
 又∵EF是AC、A1D的公共垂线,
又∵EF是AC、A1D的公共垂线,∴BD1∥EF.
故答案为:平行.
点评:本题主要考查直线与平面垂直的性质定理的应用,空间中直线与直线之间的位置关系,其中建立空间坐标系,借助向量分析直线与直线之间的位置关系是解答本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的:
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的: 已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点.
已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点. 如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.
如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积. 如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )
如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )