题目内容

已知点A在圆C：x2+(y-2)2=
1
3
上运动，点B在以F(
3
，0)为右焦点的椭圆x2+4y2=4上运动，求|AB|的最大值______．
∵|AB|≤|BC|+|CA|=|BC|+
3
3
，当且仅当B，C，A共线时取等号．
因此当|BC|最大值时，|AB|取最大值时．
设B（x，y），则 d2=|BC|2=x2+（y-2）2=4（1-y2）+（y-2）2=-3y2-4y+8=--3(y+
2
3
)2+
28
3
，
∵-1≤y≤1，∴当y=-
2
3
时，d2最大值为
28
3
，d最大值为
28
3
，
|AB|的最大值为
28
3
+
1
3
=
2
21
+
3
3

故答案为：
2
21
+
3
3
练习册系列答案
相关题目
已知点P在圆C：x2+（y-3）2=1上，点Q在
x2
5
-
x2
2
=1的右支上，F是双曲线的左焦点，则|PQ|+|QF|的最小值（　　）
已知点A在圆C：x2+(y-2)2=
1
3
上运动，点B在以F(
3
，0)为右焦点的椭圆x2+4y2=4上运动，求|AB|的最大值
2
21
+
3
3
2
21
+
3
3
．
已知点P在圆C：x2+（y-3）2=1上，点Q在=1的右支上，F是双曲线的左焦点，则|PQ|+|QF|的最小值（ ）
A．2+1
B．3+2
C．4+2
D．5+2
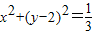已知点A在圆C：上运动，点B在以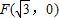为右焦点的椭圆x2+4y2=4上运动，求|AB|的最大值    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网