题目内容
(本题满分12分)
已知函数 (
(
 )
)
(1)若 从集合
从集合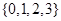 中任取一个元素,
中任取一个元素, 从集合
从集合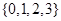 中任取一个元素,求方程
中任取一个元素,求方程 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;
(2)若 从区间
从区间 中任取一个数,
中任取一个数, 从区间
从区间 中任取一个数,求方程
中任取一个数,求方程 没有实根的概率.
没有实根的概率.
(1) (2)
(2)
解析试题分析:(1) ∵  取值的情况是:
取值的情况是:


 ,
,
(0,3),(1,3),(2,3),(3,3)其中第一个数表示 的取值,第二个数表示
的取值,第二个数表示 的取值.
的取值.
即基本事件总数为16
设“方程 恰有两个不相等的实根”为事件
恰有两个不相等的实根”为事件
当 时,方程
时,方程 恰有两个不相等实根即为b>
恰有两个不相等实根即为b> 且
且 不等于零
不等于零
当b> 时,
时, 取值的情况有(1,2),(1,3),(2,3)
取值的情况有(1,2),(1,3),(2,3)
即 包含的基本事件数为3,
包含的基本事件数为3,
∴方程 恰有两个不相等实根的概率
恰有两个不相等实根的概率 . …………………6分
. …………………6分
(2) ∵ 从区间
从区间 中任取一个数,
中任取一个数, 从区间
从区间 中任取一个数,
中任取一个数,
则试验的全部结果构成区域
这是一个矩形区域,其面积 ……………………8分
……………………8分
设“方程 没有实根”为事件B,则事件B所构成的区域为
没有实根”为事件B,则事件B所构成的区域为 其面积
其面积
 …………10分
…………10分
由几何概型的概率计算公式可得:
方程 没有实根的概率
没有实根的概率 . …………………12分
. …………………12分
考点:古典概型概率与几何概型概率
点评:古典概型概率要找到所有的基本事件种数及满足题意要求的基本事件种数,然后求其比值;几何概型概率要求出对应的面积大小,然后求其面积比

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加
四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加 岗位服务的概率;(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量
岗位服务的概率;(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量 为这五名志愿者中参加
为这五名志愿者中参加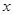 的分布列和数学期望。
的分布列和数学期望。 的一元二次方程
的一元二次方程 .
. ,
, 都是从集合
都是从集合 中任取的数字,求方程有实根的概率;
中任取的数字,求方程有实根的概率; ,科目B每次考试合格的概率为
,科目B每次考试合格的概率为 ,假设各次考试合格与否均互不影响.
,假设各次考试合格与否均互不影响. ,求随即变量
,求随即变量