题目内容
设不同直线m、n和不同平面α、β,给出下列四个命题:①
;②
;
③
m、n异面;④
其中假命题有( )
A.0个 B.1个 C.2个 D.3个
解析:①真,②③④假.
答案:D
练习册系列答案
阅读快车系列答案
相关题目
设椭圆C1、抛物线C2的焦点均在x轴上，C1的中心和C2的顶点均为原点，从每条曲线上至少取两个点，将其坐标记录于表中：
（1）求C1、C2的标准方程；
（2）设直线l与椭圆C1交于不同两点M、N，且
•
=0，请问是否存在这样的直线l过抛物线C2的焦点F？若存在，求出直线l的方程；若不存在，说明理由．
| x | 3 | -2 | 4 |
|
| ||||||||
| y | -2
|
0 | -4 |
|
-
|
（2）设直线l与椭圆C1交于不同两点M、N，且
| OM |
| ON |
，请问是否存在这样的直线l过抛物线C2的焦点F？若存在，求出直线l的方程；若不存在，说明理由．
设椭圆C1、抛物线C2的焦点均在x轴上，C1的中心和C2的顶点均为原点，从每条曲线上至少取两个点，将其坐标记录于表中：
（1）求C1、C2的标准方程；
（2）设直线l与椭圆C1交于不同两点M、N，且
，请问是否存在这样的直线l过抛物线C2的焦点F？若存在，求出直线l的方程；若不存在，说明理由．
| x | 3 | -2 | 4 |  |  |
| y | -2 | 0 | -4 |  | - |
（2）设直线l与椭圆C1交于不同两点M、N，且
，请问是否存在这样的直线l过抛物线C2的焦点F？若存在，求出直线l的方程；若不存在，说明理由．
设椭圆C1、抛物线C2的焦点均在x轴上，C1的中心和C2的顶点均为原点，从每条曲线上至少取两个点，将其坐标记录于表中：
（1）求C1、C2的标准方程；
（2）设直线l与椭圆C1交于不同两点M、N，且
，请问是否存在这样的直线l过抛物线C2的焦点F？若存在，求出直线l的方程；若不存在，说明理由．
| x | 3 | -2 | 4 |  |  |
| y | -2 | 0 | -4 |  | - |
（2）设直线l与椭圆C1交于不同两点M、N，且
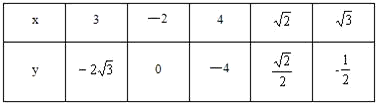
，请问是否存在这样的直线l过抛物线C2的焦点F？若存在，求出直线l的方程；若不存在，说明理由．