题目内容
已知数列{an}为等差数列,若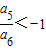 ,则数列{|an|}的最小项是第 项.
,则数列{|an|}的最小项是第 项.
【答案】分析:利用等差数列的单调性,判明正负项的分界位置(5、6之间),再比较最靠近的0的两项a5、a6的绝对值的大小.
解答:解:∵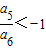 <0
<0
∴a5和a6异号,即a5和a6是正负项的分界位置
∴数列{|an|}的最小项应是靠近0较近的那项,a5或a6,
∵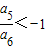
∴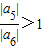 ,|a5|>|a6|
,|a5|>|a6|
∴数列{|an|}的最小项是第6项.
故答案为:6
点评:本题主要考查了等差中项的性质.即在有穷等差数列中,与首末两项距离相等的两项和相等.并且等于首末两项之和;特别的,若项数为奇数,还等于中间项的2倍,
解答:解:∵
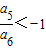 <0
<0∴a5和a6异号,即a5和a6是正负项的分界位置
∴数列{|an|}的最小项应是靠近0较近的那项,a5或a6,
∵
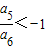
∴
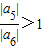 ,|a5|>|a6|
,|a5|>|a6|∴数列{|an|}的最小项是第6项.
故答案为:6
点评:本题主要考查了等差中项的性质.即在有穷等差数列中,与首末两项距离相等的两项和相等.并且等于首末两项之和;特别的,若项数为奇数,还等于中间项的2倍,

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
定义:在数列{an}中,an>0且an≠1,若
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009=( )
| a | an+1 n |
| A、6026 | B、6024 |
| C、2 | D、4 |

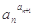 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4