题目内容
(2012•青岛一模)设变量x,y满足约束条件:
,则目标函数z=
的最小值为
.
|
| y |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
分析:先根据约束条件画出可行域,再利用目标函数的几何意义:平面区域内的一点与原点连线的斜率求最小值
解答: 解:作出可行域如图所示的阴影部分,
解:作出可行域如图所示的阴影部分,
由于z=
的几何意义是平面区域内的一点与原点连线的斜率,
结合图形可知,直线OC的斜率最小
由
可得C(2,1),此时
=
故答案为:
 解:作出可行域如图所示的阴影部分,
解:作出可行域如图所示的阴影部分,由于z=
| y |
| x |
结合图形可知,直线OC的斜率最小
由
|
| y |
| x |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查了简单的线性规划,以及利用几何意义求最值,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
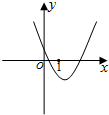 (2012•青岛一模)已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数g(x)=loga(x+b)的图象可能为
(2012•青岛一模)已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数g(x)=loga(x+b)的图象可能为