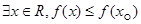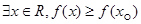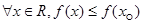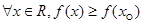题目内容
“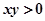 ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析: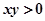 说明x,y同号,所以可以得出
说明x,y同号,所以可以得出 ,但是由
,但是由 只能得出
只能得出 ,所以“
,所以“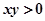 ”是“
”是“ ”的充分不必要条件.
”的充分不必要条件.
考点:本小题考查充分条件、必要条件的判定.
点评:解决此类问题,要分清条件和结论,分清是谁推出谁.

练习册系列答案
相关题目
下面是关于复数 的三个命题:
的三个命题: 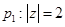
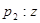 在复平面内对应的点在第四象限
在复平面内对应的点在第四象限 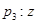 是纯虚数
是纯虚数
其中的真命题为
A. | B. | C.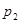 | D.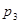 |
“函数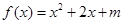 存在零点”的一个必要不充分条件是( )
存在零点”的一个必要不充分条件是( )
A.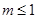 | B.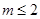 | C.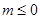 | D.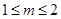 |
给出下面结论:
(1)命题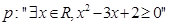 的否定为
的否定为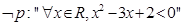 ;
;
(2)若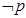 是
是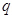 的必要不充分条件,则
的必要不充分条件,则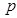 是
是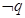 的充分不必要条件;
的充分不必要条件;
(3)“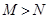 ”是“
”是“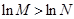 ”成立的充分不必要条件;
”成立的充分不必要条件;
(4) 若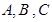 是
是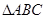 的三个内角,则“
的三个内角,则“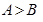 ”是“
”是“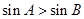 ”成立的充要条件。
”成立的充要条件。
其中正确结论的个数是
| A.4 | B.3 | C.2 | D.1 |
给出如下四个命题:
①若“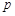 且
且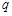 ”为假命题,则
”为假命题,则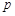 、
、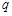 均为假命题;
均为假命题;
②命题“若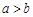 ,则
,则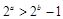 ”的否命题为“若
”的否命题为“若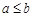 ,则
,则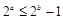 ”;
”;
③“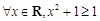 ”的否定是“
”的否定是“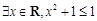 ”;
”;
④等比数列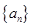 中,首项
中,首项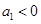 ,则数列
,则数列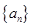 是递减数列的充要条件是公比
是递减数列的充要条件是公比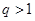 ;
;
其中不正确的命题个数是
| A.4 | B.3 | C.2 | D.1 |
设a、b、c∈R+,P=a+b-c,Q=b+c-a,R=c+a-b,则“PQR>0”是“P、Q、R同时大于零”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
对于任意实数 ,<
,< >表示不小于
>表示不小于 的最小整数,例如<1.1>=2,<
的最小整数,例如<1.1>=2,<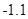 >=
>= 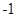 ,那么“
,那么“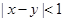 ”是“<
”是“< >=<
>=<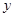 >”( ).
>”( ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
若 表示直线,
表示直线, 表示平面,且
表示平面,且 ,则“
,则“ ”是“
”是“ ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
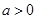 ,函数
,函数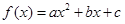 ,若
,若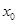 满足关于
满足关于 的方程
的方程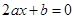 ,则下列选项的命题中为假命题的是( )
,则下列选项的命题中为假命题的是( )